
【题目】如图,正方形ABCD中,AB=![]() ,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15度.
,点E、F分别在BC、CD上,且∠BAE=30°,∠DAF=15度.
(1)求证:DF+BE=EF;
(2)求∠EFC的度数;
(3)求△AEF的面积.
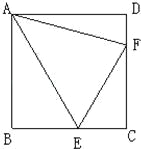
【答案】(1)见解析 (2)30° (3)![]()
【解析】试题分析:
(1)延长EB至点G,使BG=DF,连接AG,由已知条件易证△ABG≌△ADF,再证△FAE≌△GAE,即可得到EF=EG=GB+BE=DF+BE;
(2)由在△ADF中,∠D=90°,∠DAF=15°,可得∠AFD=90°-15°=75°,结合△ABG≌△ADF,△AGE≌△AFE,可得AFE=∠AGE=∠AFD=75°,由此即可得到∠EFC=30°;
(3)在△ABE中由已知条件易得BE=1,CE=![]() ,结合△EFC中∠EFC=30°,∠C=90°,可得CF=
,结合△EFC中∠EFC=30°,∠C=90°,可得CF=![]() ,由此即可求得△ECF的面积;由△ABG≌△ADF,△FAE≌△GAE,结合由S△AEF=S正方形ABCD-S△ADF-S△AEB-S△CEF,即可得到S△AEF=
,由此即可求得△ECF的面积;由△ABG≌△ADF,△FAE≌△GAE,结合由S△AEF=S正方形ABCD-S△ADF-S△AEB-S△CEF,即可得到S△AEF=![]() (S正方形ABCD-S△CEF),由此即可求得△AEF的面积了.
(S正方形ABCD-S△CEF),由此即可求得△AEF的面积了.
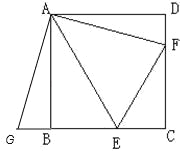
试题解析:
(1)延长EB至G,使BG=DF,连接AG,
∵正方形ABCD,
∴AB=AD,∠ABG=∠ADF=∠BAD=90°,
∵BG=DF,
∴△ABG≌△ADF,
∴AG=AF,
∵∠BAE=30°,∠DAF=15°,
∴∠FAE=∠GAE=45°,
∵AE=AE,
∴△FAE≌△GAE,
∴EF=EG=GB+BE=DF+BE;
(2)∵在△ADF中,∠D=90°,∠DAF=15°,
∴∠AFD=90°-15°=75°,
∵△ABG≌△ADF,△AGE≌△AFE,
∴∠AFE=∠AGE=∠AFD=75°,
∴∠EFC=180°-∠DFA-∠AFE=180°-75°-75°=30°;
(3)∵AB=BC=![]() ,∠BAE=30°,
,∠BAE=30°,
∴BE=1,CE=![]() -1,
-1,
∵∠EFC=30°,
∴CF=3-![]() ,
,
∴S△CEF=![]() CECF=2
CECF=2![]() -3,
-3,
由(1)知,△ABG≌△ADF,△FAE≌△GAE,
∴S△AEF=S正方形ABCD-S△ADF-S△AEB-S△CEF=S正方形ABCD-S△AEF-S△CEF,
∴S△AEF=![]() (S正方形ABCD-S△CEF)=
(S正方形ABCD-S△CEF)=![]() 3-
3-![]() .
.



科目:初中数学 来源: 题型:
【题目】学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共40kg,了解到这些蔬菜的种植成本共42元,还了解到如下信息:

(1)请问采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
人 数 | 1 | 4 | 3 | 2 | 2 |
(1)这个队队员年龄的众数是 ,中位数是 ;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为ABC的AB边上一点,E为AC延长线上的一点,且CE=BD。
(1)当AB=AC时,求证:DE>BC
(2)当AB≠AC时,DE与BC有何大小关系?给出结论,画出图形,并证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE与DF的数量关系,并证明你的结论.
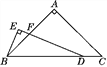
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查方式,不适合使用全面调查的是( )
A. 旅客上飞机前的安检B. 航天飞机升空前的安检
C. 了解全班学生的体重D. 了解咸宁市中学生每天使用手机的时间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com