
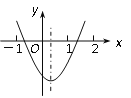
【题目】如图,抛物线y=ax2+bx+c的对称轴是![]() ,小亮通过观察得出了下面四条信息:
,小亮通过观察得出了下面四条信息:
①c<0,②abc<0,③a-b+c>0,④2a-3b=0.你认为其中正确的有________.(填序号)
【答案】①③.
【解析】
利用二次函数的图形和性质,结合抛物线的开口方向,对称轴,以及抛物线与坐标轴的交点对每个命题进行判断.
解:当x=0时,y=c,因为抛物线与y轴的交点在y轴的负半轴,所以c<0,故①正确.
∵抛物线的开口向上,
∴a>0.
∵对称轴x=-![]() =
=![]() ,
,
∴b=-![]() <0.
<0.
∴abc>0.故②错误.
当x=-1时,y=a-b+c,由图形可知:a-b+c>0,故③正确.
由对称轴得:-![]() =
=![]() ,
,
∴2a+3b=0.而不是2a-3b=0,故④错误.
故答案是:①③.
本题考查的是二次函数的图形与系数的关系,由开口方向得到a的正负,由抛物线与y轴的交点得到c的正负,由对称轴得到b的正负,再用抛物线与x的交点得到a-b+c>0,对所给的四个命题作出判断.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D是圆上两点,且OD∥AC,OD与BC交于点E.

(1)求证:E为BC的中点;
(2)若BC=8,DE=3,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
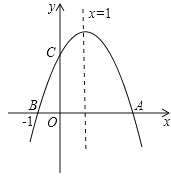
【题目】如图,二次函数 y=ax2+bx+c(a≠0)的图象与 x 轴交于 A、B 两点,与 y 轴交于点 C,且对称轴为直线 x=1, 点 B 的坐标为(-1,0).则下面的五个结论:①2a+b=0;②abc>0;③当 y<0 时,x<-1 或 x>2;④c<4b;⑤ a+b>m(am+b)(m≠1),其中正确的个数是( )
A. 2 个 B. 3个 C. 4 个 D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
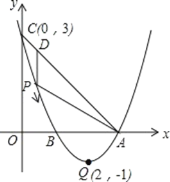
【题目】如图,已知抛物线 y=ax2+bx+c(a≠0)的顶点坐标为 Q(2,﹣1),且与 y 轴交于点 C(0,3), 与 x 轴交于 A、B 两点(点 A 在点 B 的右侧),点 P 是抛物线上的一动点,从点 C 沿抛物线向 点 A 运动(点 P 与 A 不重合),过点 P 作 PD∥y 轴,交 AC 于点 D.
(1)求该抛物线的函数关系式及 A、B 两点的坐标;
(2)求点 P 在运动的过程中,线段 PD 的最大值;
(3)若点 P 与点 Q 重合,点 E 在 x 轴上,点 F 在抛物线上,问是否存在以 A,P,E,F 为顶 点的平行四边形?若存在,直接写出点 F 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
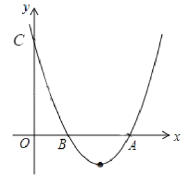
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:① b2-4ac>0;② 2a+b<0;③ 4a-2b+c=0;④ a︰b︰c= -1︰2︰3.其中正确的是【 】
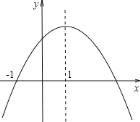
(A) ①② (B) ②③ (C) ③④ (D)①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com