
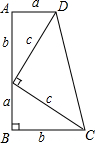
 勾股定理的证明方法很多,下面是美国第20任总统加菲尔德用此图证明了勾股定理,你也来用此图试一试,验证:a2+b2=c2.
勾股定理的证明方法很多,下面是美国第20任总统加菲尔德用此图证明了勾股定理,你也来用此图试一试,验证:a2+b2=c2. 分析 因为梯形的上底为a,下底为b,高为(a+b),则它的面积可表示为$\frac{1}{2}$(a+b)•(a+b);此梯形的面积还可以看成是三个直角三角形的面积和,即$\frac{1}{2}$(ab×2+c2);则$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(ab×2+c2),进而得出即可.
解答 证明:由题意可知梯形面积为$\frac{1}{2}$(a+b)(a+b);
此梯形的面积还可以看成是三个直角三角形的面积和,即$\frac{1}{2}$(ab×2+c2).
因此$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(ab×2+c2),
即a2+b2=c2.
点评 此题主要考查了勾股定理的证明,主要应用梯形的面积公式和三角形的面积公式得出是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 排数 | 每排座位数 |
| 1 | 18 |
| 2 | 20 |
| 3 | 22 |
| 4 | 24 |
| 5 | 26 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com