
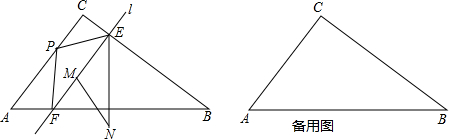
分析 (1)①由条件可以求出AB=10,根据P点在各边的速度可以求出在各边所用的时间,从而可以求出P在3秒内走的路程;
②根据CE等于点P走的路程与AC的差建立方程就可以求出t的值;
③若PE∥AB,则△CPE∽△CAB,根据相似三角形的性质建立方程,就可求出t的值.
(2)由题意可得∠CPE=∠PEF=∠MEN,又由EN⊥AB,∠FEB=∠C=90°可得∠B=∠MEN,则有∠CPE=∠B,从而得到△CPE∽△CBA,根据相似三角形的性质建立方程,就可求出t的值.
(3)由于点P在三条线段上运动,因此需分点P在AC、BC及AB上三种情况进行讨论,然后根据菱形的性质和相似三角形的性质建立关于t的方程就可求出t的值.
解答 解:(1)①在Rt△ABC中,由∠C=90°,AC=6,BC=8得AB=10.
∵点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位,
∴点P在AC边上运动的时间为:6÷3=2秒,
点P在BC边上运动的时间为:8÷4=2秒,
点P在AB边上运动的时间为:10÷5=2秒.
∴当t=3秒时,点P走过的路径长为6+4×(3-2)=10.
②由题意可知:当(t-2)×4=$\frac{4}{3}$t时,点P与点E重合.
解得:t=3.
∴t=3秒时,点P与点E重合.
③若PE∥AB,如图1,
则有△CPE∽△CAB.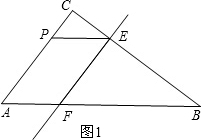
∴$\frac{CP}{CA}$=$\frac{CE}{CB}$.
∴CP•CB=CE•CA.
∵CP=6-3t,CB=8,CE=$\frac{4}{3}$t,CA=6,
∴8(6-3t)=$\frac{4}{3}$t×6.
解得:t=1.5.
∴当t=1.5秒时,PE∥AB.
故答案分别为:10、3、1.5.
(2)如图2,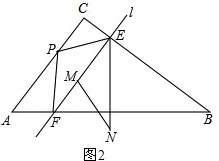 由旋转可得:∠PEF=∠MEN,
由旋转可得:∠PEF=∠MEN,
∵P在AC上,
∴AP=3t (0<t≤2).
∴CP=6-3t.
∵EF∥AC,∠C=90°,
∴∠CPE=∠PEF,∠BEF=∠C=90°.
∵EN⊥AB,
∴∠B=90°-∠NEB=∠MEN.
∴∠CPE=∠B.
∵∠C=∠C,∠CPE=∠B,
∴△CPE∽△CBA.
∴$\frac{CP}{CB}$=$\frac{CE}{CA}$.
∴CP•CA=CE•CB.
∴(6-3t)×6=$\frac{4t}{3}$×8.
解得:t=$\frac{54}{43}$.
∴当EN⊥AB时,t的值为$\frac{54}{43}$(秒).
(3)①当P点在AC上时,(0<t≤2),如图3,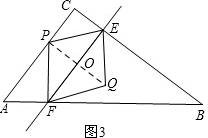 ∵EF∥AC,
∵EF∥AC,
∴△FEB∽△ACB,
∴$\frac{EF}{AC}$=$\frac{BF}{BA}$=$\frac{BE}{BC}$.
∵AC=6,BC=8,AB=10,BE=8-$\frac{4t}{3}$,
∴EF=6-t,BF=10-$\frac{5t}{3}$.
∵四边形PEQF是菱形,
∴∠POE=90°,EF=2OE.
∵∠C=∠POE=∠OEC=90°,
∴四边形PCEO是矩形.
∴OE=PC.
∴EF=2PC.
∴6-t=2(6-3t).
∴t=$\frac{6}{5}$.
②当P点在BC上时,
此时点Q也在BC上,
所以以点P、E、Q、F为顶点不能构成菱形,故不存在.
③当P在AB上时,(4<t<6),如图4,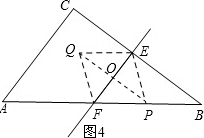 ∵四边形PFQE是菱形,
∵四边形PFQE是菱形,
∴OE=OF=$\frac{1}{2}$EF,EF⊥PQ.
∴∠FOP=90°=∠FEB.
∴OP∥BE.
∴△FOP∽△FEB.
∴$\frac{FP}{BF}$=$\frac{FO}{FE}$.
∴$\frac{FP}{BF}$=$\frac{1}{2}$.
∴BF=2PF.
∴BF=2BP.
∵BF=10-$\frac{5}{3}$t,BP=5(t-4),
∴10-$\frac{5t}{3}$=2[5(t-4)].
解得:t=$\frac{30}{7}$.
综上所述:当四边形PEQF为菱形时,t的值为$\frac{6}{5}$或$\frac{30}{7}$.
点评 本题考查了相似三角形的判定及性质、矩形的判定与性质、菱形的性质、旋转的性质、勾股定理等知识,还考查了分类讨论的思想,利用相似三角形的性质和菱形的性质是解答本题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
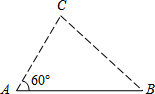 小彬和小红分别在平坦的冰面上的点A和点B处.如图,点A和点B之间的距离是100米,小彬离开点A以每秒8米的速度沿着与AB成60°角的直线滑行,在小彬离开点A的同时,小红以每秒7米的速度也沿着一条直线滑行离开点B,这条直线能使小彬与小红以所给的速度最早相遇的时间是多少秒?
小彬和小红分别在平坦的冰面上的点A和点B处.如图,点A和点B之间的距离是100米,小彬离开点A以每秒8米的速度沿着与AB成60°角的直线滑行,在小彬离开点A的同时,小红以每秒7米的速度也沿着一条直线滑行离开点B,这条直线能使小彬与小红以所给的速度最早相遇的时间是多少秒?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com