
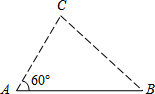
 小彬和小红分别在平坦的冰面上的点A和点B处.如图,点A和点B之间的距离是100米,小彬离开点A以每秒8米的速度沿着与AB成60°角的直线滑行,在小彬离开点A的同时,小红以每秒7米的速度也沿着一条直线滑行离开点B,这条直线能使小彬与小红以所给的速度最早相遇的时间是多少秒?
小彬和小红分别在平坦的冰面上的点A和点B处.如图,点A和点B之间的距离是100米,小彬离开点A以每秒8米的速度沿着与AB成60°角的直线滑行,在小彬离开点A的同时,小红以每秒7米的速度也沿着一条直线滑行离开点B,这条直线能使小彬与小红以所给的速度最早相遇的时间是多少秒?  优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
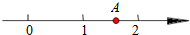 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )| A. | $\frac{3}{2}$sin30°<x<sin60° | B. | cos30°<x<$\frac{3}{2}$cos45° | ||
| C. | $\frac{3}{2}$tan30°<x<tan45° | D. | $\frac{3}{2}$tan45°<x<tan60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格里,以格点为顶点按要求画图,并回答问题.
在如图所示的正方形网格里,以格点为顶点按要求画图,并回答问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com