
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.

(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
【答案】(1)详见解析;(2)详见解析;(3)四边形ABNE是正方形,理由详见解析.
【解析】
试题分析:(1)根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,求得∠ABF=135°,∠ABF=∠ACD,再证得BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;(2)由(1)知AF=AD,△ABF≌△ACD,得出∠FAB=∠DAC,证出∠EAF=∠BAD,由SAS证明△AEF≌△ABD,得出对应边相等即可;(3)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
试题解析:(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°,
∵∠BCD=90°,
∴∠ABF=∠ACD,
∵CB=CD,CB=BF,∴BF=CD,
在△ABF和△ACD中,
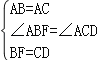 ,
,
∴△ABF≌△ACD(SAS),
∴AD=AF;
(2)证明:由(1)知,AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC,
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD,
在△AEF和△ABD中,
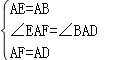 ,
,
∴△AEF≌△ABD(SAS),
∴BD=EF;
(3)解:四边形ABNE是正方形;理由如下:
∵CD=CB,∠BCD=90°,
∴∠CBD=45°,
由(2)知,∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°,
∴四边形ABNE是矩形,
又∵AE=AB,
∴四边形ABNE是正方形.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将点P(-2,3)沿x轴方向向右平移3个单位得到点Q,则点Q的坐标是( )
A.(-2,6)
B.(-2,0)
C.(1,3)
D.(-5,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆桥?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知第二象限内的点P,到x轴的距离为2,到y轴的距离为3,则点P关于原点的对称点的坐标为( )
A.(-3,2)
B.(3,-2)
C.(2,-3)
D.(-2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正
整数,满分为![]() 分)进行统计,已知
分)进行统计,已知![]() 组的频数
组的频数![]() 比
比![]() 组的频数
组的频数![]() 小,绘制统计频数分别直方图(未完成)
小,绘制统计频数分别直方图(未完成)
和扇形统计图如下,
请解答下列问题:
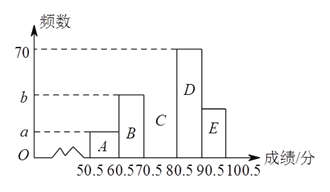
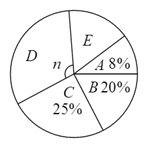
(![]() )样本容量为:__________,
)样本容量为:__________, ![]() 为__________.
为__________.
(![]() )
)![]() 为__________,
为__________, ![]() 组所占比例为__________
组所占比例为__________![]() .
.
(![]() )补全频数分布直方图.
)补全频数分布直方图.
(![]() )若成绩在
)若成绩在![]() 分以上记作优秀,全校共有
分以上记作优秀,全校共有![]() 名学生,估计成绩优秀学生有__________名.
名学生,估计成绩优秀学生有__________名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:C+F=1B,19﹣F=A,18÷4=6,则A×B=( )
A. 72 B. 6E C. 5F D. B0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com