
【题目】如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB上有一点R.若△PQR周长最小,则最小周长是( )

A.10 B.15 C.20 D.30
【答案】A
【解析】
试题分析:先画出图形,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.再根据线段垂直平分线的性质得出△PQR=EF,再根据三角形各角之间的关系判断出△EOF的形状即可求解.
解:设∠POA=θ,则∠POB=30°﹣θ,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.
作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.
连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.
∵OA是PE的垂直平分线,
∴EQ=QP;
同理,OB是PF的垂直平分线,
∴FR=RP,
∴△PQR的周长=EF.
∵OE=OF=OP=10,且∠EOF=∠EOP+∠POF=2θ+2(30°﹣θ)=60°,
∴△EOF是正三角形,∴EF=10,
即在保持OP=10的条件下△PQR的最小周长为10.
故选A.



科目:初中数学 来源: 题型:
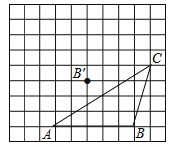
【题目】如图在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为______;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系是______;
(4)在图中画出△ABC的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.经过两点有且只有一条直线
B.三角形的中位线平行且等于第三边的一半
C.平行四边形的对角线相等
D.圆的切线垂直于经过切点的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队修建一条总长为1860米的公路,在使用旧设备施工17天后,为尽快完成任务,工程队引进了新设备,从而将工作效率提高了50%,结果比原计划提前15天完成任务.
(1)工程队在使用新设备后每天能修路多少米?
(2)在使用旧设备和新设备工作效率不变的情况下,工程队计划使用旧设备m天,使用新设备n(16≤n≤26)天修建一条总长为1500米的公路,使用旧设备一天需花费16000元,使用新设备一天需花费25000元,当m、n分别为何值时,修建这条公路的总费用最少,并求出最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A(m,﹣2)、B(1,n﹣m)关于x轴对称,则m、n的值为( )
A. m=1,n=1 B. m=﹣1,n=1 C. m=1,n=3 D. m=1,n=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着居民经济收入的不断提高以及汽车业的快速发展,家用汽车已越来越多地进入普通家庭,抽样调查显示,截止2015年底某市汽车拥有量为16.9万辆.己知2013年底该市汽车拥有量为10万辆,设2013年底至2015年底该市汽车拥有量的平均增长率为x,根据题意列方程得( )
A.10(1+x)2=16.9 B.10(1+2x)=16.9 C.10(1﹣x)2=16.9 D.10(1﹣2x)=16.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com