练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

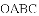
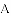
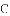
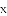
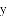
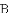
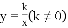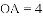
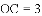
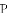
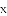
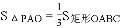    如图，矩形的顶点、分别在、轴的正半轴上，点在反比例函数的第一象限内的图像上，，，动点在轴的上方，且满足.

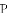
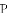
    （1）若点在这个反比例函数的图像上，求点的坐标；

    （2）连接、，求的最小值；

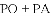
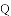
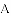
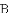
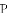
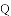
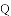
    （3）若点是平面内一点，使得以、、、为顶点的四边形是菱形，则请你直接写出满足条件的所有点的坐标.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：吉林省长春市2017-2018九年级数学一模试卷 题型：解答题

    已知关于x的二次函数的图象与x轴有2个交点.

    （1）求k的取值范围；

    （2）若图象与x轴交点的横坐标为，且它们的倒数之和是，求k的值.

    查看答案和解析>>

    科目：初中数学 来源：北京市2017--2018第二学期期中考试数学试卷 题型：单选题

    《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架，书中的算法体系至今仍在推动着计算机的发展和应用. 《九章算术》中记载：今有户不知高、广，竿不知长、短.横之不出四尺，从之不出二尺，邪之适出.问户高、广、邪各几何？

    译文是：今有门，不知其高、宽，有竿，不知其长、短. 横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等.问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程为（ ）

    A. ( x-4)2+(x-2)2 =x2 B. ( x+4)2=x2+(x-2)2

    C. ( x-4)2=x2+(x+2)2 D. ( x+4)2=x2+(x+2)2

    查看答案和解析>>

    科目：初中数学 来源：云南省2018年中考数学试卷 题型：单选题

    在Rt△ABC中，∠C=90°，AC=1，BC=3，则∠A的正切值为（　　）

    A. 3 B. C. D.

    查看答案和解析>>

    科目：初中数学 来源：云南省2018年中考数学试卷 题型：填空题

    如图，已知AB∥CD，若，则=_____．

    查看答案和解析>>

    科目：初中数学 来源：江苏省宿迁市宿豫区2017-2018学年八年级下期末数学试卷 题型：解答题

    为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制了如下尚不完整的统计图表:

    调查结果统计表

    调查结果频数分布直方图 调查结果扇形统计图

    请根据以上图表，解答下列问题：

    （1）填空：这次调查的样本容量是 ， , ；

    （2）补全频数分布直方图；

    （3）求扇形统计图中扇形的圆心角度数；

    （4）该校共有人，请估计每月零花钱的数额在范围的人数.

    查看答案和解析>>

    科目：初中数学 来源：江苏省宿迁市宿豫区2017-2018学年八年级下期末数学试卷 题型：填空题

    如图，曲线是由函数在第一象限内的图像绕坐标原点逆时针旋转得到的，且与轴交于点，则点的坐标为_____.

    查看答案和解析>>

    科目：初中数学 来源：河南省平顶山市招调研试卷（一） 题型：解答题

    如图1，正方形ABCD和正方形AEFG，连接DG，BE。

    (1)发现

    当正方形AEFG绕点A旋转，如图2，①线段DG与BE之间的数量关系是____________。②直线DG与直线BE之间的位置关系是____________。

    (2)探究

    如图3，若四边形ABCD与四边形AEFG都为矩形，且AD=2AB，AG=2AE，证明：直线DG⊥BE

    (3)应用

    在(2)情况下，连结GE(点E在AB上方)，若GE∥AB，且AB=，AE=1，则线段DG是多少?(直接写出结论)

    查看答案和解析>>

    科目：初中数学 来源：湖北省咸宁市2018年中考数学试卷 题型：单选题

    用4个完全相同的小正方体搭成如图所示的几何体，该几何体的（　　）

    A. 主视图和左视图相同 B. 主视图和俯视图相同

    C. 左视图和俯视图相同 D. 三种视图都相同

    查看答案和解析>>

    同步练习册答案