
科目:初中数学 来源: 题型:填空题
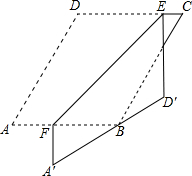 如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.
如图,在?ABCD纸片中,∠A=60°,AD-AB=1,点E,F分别在边CD,AB上,将纸片沿EF折叠,使点A,D分别落在点A′,D′,处,且AD经过点B.当D′E⊥CD时,CE=1,则AB的长是$\frac{3\sqrt{3}+5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
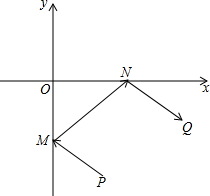 牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.
牧马人某天要从马厩牵出马,先到草地边的某一处牧马,再到河边饮水,然后回到帐篷,为了便于研究,以河边为x轴、草地边为y轴建立平面直角坐标系,如图所示,马厩P的坐标为(2,-4),帐篷Q的坐标为(6,-2),请你帮他确定这一天的最短路线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
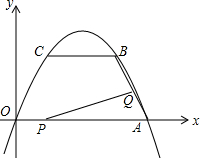 已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.
已知抛物线y=ax2+bx+c经过O(0,0),A(4,0),B(3,$\sqrt{3}$)三点,连结AB,过点B作BC∥x轴交该抛物线于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
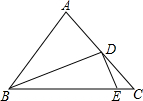 如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )
如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD,垂足为D,DE交BC于点E.若DE=5,BD=12,则CD的长为( )| A. | 6 | B. | 6.5 | C. | 7 | D. | 7.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
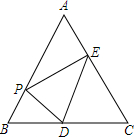 如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F.
如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com