已知等腰三角形的两条边分别为5,6,求一腰上的高线长.
解:
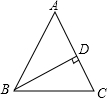
△ABC中,AB=AC,
设AD=x,
分为两种情况:①当AB=AC=5,BC=6时,
则CD=5-x,
∵在Rt△ABD和Rt△CDB中,由勾股定理得:BD
2=AB
2-AD
2=BC
2-CD
2,
∴5
2-x
2=6
2-(5-x)
2,
x=

,
∴BD
2=5
2-(

)
2,
∴BD=

,
②当AB=AC=6,BC=5时,
则CD=6-x,
∵在Rt△ABD和Rt△CDB中,由勾股定理得:BD
2=AB
2-AD
2=BC
2-CD
2,
∴6
2-x
2=5
2-(6-x)
2,
x=
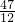
,
∴BD
2=6
2-(
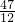
)
2,
∴BD=
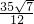
;
即一腰上的高线长是

或
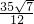
.
分析:设AD=x,分为两种情况:①当AB=AC=5,BC=6时,②当AB=AC=6,BC=5时,由勾股定理得:BD
2=AB
2-AD
2=BC
2-CD
2,代入求出x,把x的值代入BD
2=AB
2-AD
2求出即可.
点评:本题考查了等腰三角形的性质,勾股定理等知识点,主要考查学生的计算能力和推理能力,注意有两个解.


 ,
, )2,
)2, ,
,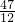 ,
,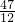 )2,
)2,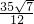 ;
; 或
或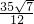 .
.
