
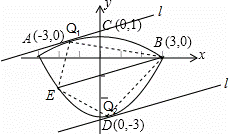
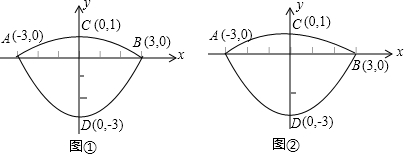
���dz����ij��˹����Ƕ����������棬�������ĺ��ĵ��ݶ�����������������϶��ɵķ��ͼ�Σ��������Ϊ�����ߡ�������ֱ��Ϊ6dm������3dm�����Ǹ�1dm������ֱ�������ֱ����Ϊ��ͬ��������ֱ������ϵ��ͼ����ʾ������ѹ��ݶ���������ߵļ�ΪC1![]() ���ѹ����ݶ����������ΪC2��
���ѹ����ݶ����������ΪC2��
��1����C1��C2�Ľ���ʽ��
��2����ͼ�ڣ�����B��ֱ��BE��y=![]() x﹣1��C1�ڵ�E��﹣2��﹣
x﹣1��C1�ڵ�E��﹣2��﹣![]() ��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ
��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ
��3�������2���е�ֱ��BE���ֲ��䣬������C1��C2���Ƿ����һ��Q��ʹ�á�EBQ�������������ڣ����Q������͡�EBQ��������ֵ���������ڣ���˵�����ɣ�

���㣺
���κ����ۺ��⡣
ר�⣺
ѹ���⣻�������ۡ�
������
��1����֪A��B��C��D�ĵ����꣬���ô���ϵ��������ȷ���������Ľ���ʽ��
��2������ֱ��BE��y=![]() x﹣1֪����ֱ�߱ع���0��﹣1���㣬��ô��EBO=��CBO�����Ե�P��B��CΪ����ġ�PBC���BOE���ƣ���ô�������Ӧ�ǵĶ�Ӧ�߱سɱ����������BC��BO��BE�ij���Ȼ�����������߶μ�ı�����ϵ���BP�ij��������õ�OP�ij�������ȷ��P�����꣮
x﹣1֪����ֱ�߱ع���0��﹣1���㣬��ô��EBO=��CBO�����Ե�P��B��CΪ����ġ�PBC���BOE���ƣ���ô�������Ӧ�ǵĶ�Ӧ�߱سɱ����������BC��BO��BE�ij���Ȼ�����������߶μ�ı�����ϵ���BP�ij��������õ�OP�ij�������ȷ��P�����꣮
��3����EBQ�У�BE��Ϊ��ֵ������BEΪ�ף�����EBQ��������ʱ��Q��ֱ��BE�ľ���������ڵ�Q������������C1��C2�ϣ�������������Ҫ��һ�£����ͨ���Ƚϵõ���ʹ��EBQ�������Q�㣮������ֱ��l��BE���ֱ���ֱ��l��������C1��C2���ҽ���һ�����㣬��ô����������Q����������������У����������������ֱ�ֱ��BE�ľ��룬������߷����������ɴ˿ɵõ�Q������͡�EBQ��������ֵ��
���
�⣺��1������������C1��C2������A��﹣3��0����B��3��0�����������ǵĽ���ʽΪ��y=a��x﹣3����x+3����
������C1������D��0��﹣3�������У�
﹣3=a��0﹣3����0+3����a=![]()
����������C1��y=![]() x2﹣3��﹣3��x��3����
x2﹣3��﹣3��x��3����
������C2������A��0��1��������
1=a��0﹣3����0+3����a=﹣![]()
����������C2��y=﹣![]() x2+1��﹣3��x��3����
x2+1��﹣3��x��3����
��2������ֱ��BE��y=![]() x﹣1�ع���0��﹣1�������ԡ�CBO=��EBO��tan��CBO=tan��EBO=
x﹣1�ع���0��﹣1�������ԡ�CBO=��EBO��tan��CBO=tan��EBO=![]() ����
����
��E�������֪��tan��AOE��![]() ������AOE�١�CBO���������ǵIJ��ǡ�EOB�١�CBx��
������AOE�١�CBO���������ǵIJ��ǡ�EOB�١�CBx��
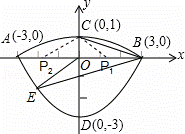
���Ե�P��B��CΪ����ġ�PBC���BOE���ƣ�ֻ�迼�����������
�١�CBP1=��EBO����OB��BE=BP1��BC������
3��![]() =BP1��
=BP1��![]() ���ã�BP1=
���ã�BP1=![]() ��OP1=OB﹣BP1=
��OP1=OB﹣BP1=![]() ��
��
��P1��![]() ��0����
��0����
�ڡ�P2BC=��EBO����BC��BP2=OB��BE������
![]() ��BP2=3��
��BP2=3��![]() ���ã�BP2=
���ã�BP2=![]() ��OP2=BP2﹣OB=
��OP2=BP2﹣OB=![]() ��
��
��P2��﹣![]() ��0����
��0����
���ϣ�����������P���У�P1��![]() ��0����P2��﹣
��0����P2��﹣![]() ��0����
��0����
��3����ͼ����ֱ��l��ֱ��BE����ֱ��l��y=![]() x+b��
x+b��
�ٵ�ֱ��l��������C1ֻ��һ������ʱ��
![]() x+b=
x+b=![]() x2﹣3������x2﹣x﹣��3b+9��=0
x2﹣3������x2﹣x﹣��3b+9��=0
��ý���Q2��![]() ��﹣
��﹣![]() ����
����
Q2��ֱ�� BE��![]() x﹣y﹣1=0 �ľ��룺
x﹣y﹣1=0 �ľ��룺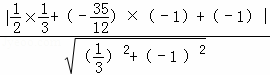 =
=![]() =
=![]() ��
��
�ڵ�ֱ��l��������C2ֻ��һ������ʱ��
![]() x+b=﹣
x+b=﹣![]() x2+1������x2+3x+9b﹣9=0
x2+1������x2+3x+9b﹣9=0
��ý���Q1��﹣![]() ��
��![]() ����
����
Q1��ֱ�� BE��![]() x﹣y﹣1=0 �ľ��룺
x﹣y﹣1=0 �ľ��룺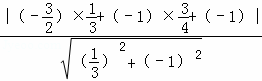 =
=![]() ��
��
�����������Q��ΪQ1��﹣![]() ��
��![]() ����
����
��EBQ����������Smax=![]() ��BE��
��BE��![]() =
=![]() ��
��
������
�����˶��κ����ۺ��⣮������ѶȺͼ��������Ƚϴ��漰�˺�������ʽ��ȷ�������������ε��ж������ʡ�ͼ������Ľⷨ���ص�֪ʶ�����2����ʱ��Ӧע��ֲ�ͬ�Ķ�Ӧ�����������ۣ�����©�⣮��3�����ѶȽϴ㵽ֱ�ߵľ��빫ʽ���㣨x0��y0����ֱ�ߣ�Ax+By+C=0���ľ���Ϊ��d=![]() ������Ҫ��ס�����ݣ����⣬��Ŀ�����ʱ�����һ��������Ԫ�أ���ʽ��Ϊ��ӱ��
������Ҫ��ס�����ݣ����⣬��Ŀ�����ʱ�����һ��������Ԫ�أ���ʽ��Ϊ��ӱ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| 3 |
| 5 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���п����� ���ͣ������
 ���ѹ����ݶ����������ΪC2��
���ѹ����ݶ����������ΪC2�� x��1��C1�ڵ�E����2����
x��1��C1�ڵ�E����2���� ��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ
��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ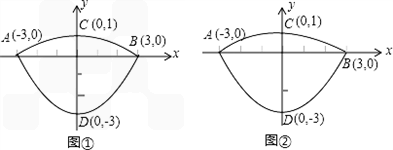
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012����б�ҵ��ѧ���ԣ���������������ѧ���������� ���ͣ������
���dz����ij��˹����Ƕ����������棬�������ĺ��ĵ��ݶ�����������������϶��ɵķ��ͼ�Σ��������Ϊ�����ߡ�������ֱ��Ϊ6dm������3dm�����Ǹ�1dm������ֱ�������ֱ����Ϊ��ͬ��������ֱ������ϵ��ͼ����ʾ������ѹ��ݶ���������ߵļ�ΪC1���ѹ����ݶ����������ΪC2��
��1����C1��C2�Ľ���ʽ��
��2����ͼ�ڣ�����B��ֱ��BE��y=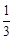 x��1��C1�ڵ�E����2����
x��1��C1�ڵ�E����2����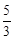 ��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ
��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ
��3�������2���е�ֱ��BE���ֲ��䣬������C1��C2���Ƿ����һ��Q��ʹ�á�EBQ�������������ڣ����Q������͡�EBQ��������ֵ���������ڣ���˵�����ɣ�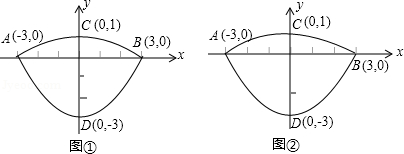
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�����ʡ�������п���ѧ�Ծ��������棩 ���ͣ������
 x-1��C1�ڵ�E��-2��-
x-1��C1�ڵ�E��-2��- ��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ
��������OE��BC����x������һ��P��ʹ�Ե�P��B��CΪ����ġ�PBC���BOE���ƣ����P������ꣻ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com