
 ,把锅盖纵断面的抛物线记为C2。
,把锅盖纵断面的抛物线记为C2。 x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣ ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;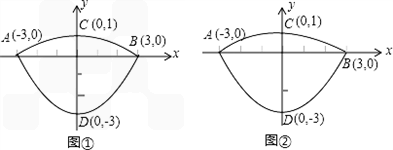
| 解:(1)由于抛物线C1、C2都过点A(﹣3,0)、B(3,0), 可设它们的解析式为:y=a(x﹣3)(x+3); 抛物线C1还经过D(0,﹣3), 则有:﹣3=a(0﹣3)(0+3),a=  即:抛物线C1:y=  x2﹣3(﹣3≤x≤3); x2﹣3(﹣3≤x≤3);抛物线C2还经过A(0,1),则有:1=a(0﹣3)(0+3),a=﹣  即:抛物线C2:y=﹣  x2+1(﹣3≤x≤3); x2+1(﹣3≤x≤3);(2)由于直线BE:y=  x﹣1必过(0,﹣1), x﹣1必过(0,﹣1),所以∠CBO=∠EBO(tan∠CBO=tan∠EBO=  ); );由E点坐标可知:tan∠AOE≠  ,即∠AOE≠∠CBO, ,即∠AOE≠∠CBO,所以它们的补角∠EOB≠∠CBx; 若以点P、B、C为顶点的△PBC与△BOE相似,只需考虑两种情况: ①∠CBP1=∠EBO,且OB:BE=BP1:BC, 即:3:  =BP1: =BP1: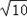 ,得:BP1= ,得:BP1= ,OP1=OB﹣BP1= ,OP1=OB﹣BP1= ; ;∴P1(  ,0); ,0);②∠P2BC=∠EBO,且BC:BP2=OB:BE, 即:  :BP2=3: :BP2=3: ,得:BP2= ,得:BP2= ,OP2=BP2﹣OB= ,OP2=BP2﹣OB=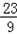 ; ;∴P2(﹣ 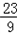 ,0), ,0),综上,符合条件的P点有:P1(  ,0)、P2(﹣ ,0)、P2(﹣ ,0); ,0);(3)如图,作直线l∥直线BE,设直线l:y=  x+b; x+b;①当直线l与抛物线C1只有一个交点时:  x+b= x+b= x2﹣3, x2﹣3,即:x2﹣x﹣(3b+9)=0 ∴该交点Q2(  ,﹣ ,﹣ ); );Q2到直线 BE:  x﹣y﹣1=0 的距离: x﹣y﹣1=0 的距离: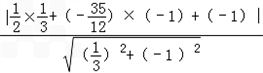 = =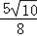 = =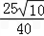 ; ;②当直线l与抛物线C2只有一个交点时:  x+b=﹣ x+b=﹣ x2+1, x2+1,即:x2+3x+9b﹣9=0 ∴该交点Q1(﹣  , , ); );Q1到直线 BE:  x﹣y﹣1=0 的距离: x﹣y﹣1=0 的距离: = = ; ;∴符合条件的Q点为Q1(﹣  , , ); );△EBQ的最大面积:Smax=  ×BE× ×BE×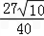 = = 。 。 |
  |


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
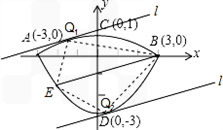
我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直接坐标系如图①所示,如果把锅纵断面的抛物线的记为C1![]() ,把锅盖纵断面的抛物线记为C2.
,把锅盖纵断面的抛物线记为C2.
(1)求C1和C2的解析式;
(2)如图②,过点B作直线BE:y=![]() x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣![]() ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖南岳阳卷)数学(带解析) 题型:解答题
我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直接坐标系如图①所示,如果把锅纵断面的抛物线的记为C1,把锅盖纵断面的抛物线记为C2.
(1)求C1和C2的解析式;
(2)如图②,过点B作直线BE:y=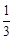 x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣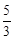 ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.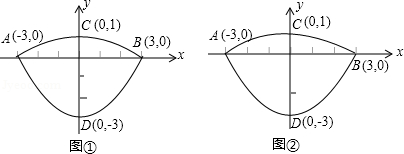
查看答案和解析>>
科目:初中数学 来源:2012年湖南省岳阳市中考数学试卷(解析版) 题型:解答题
 x-1交C1于点E(-2,-
x-1交C1于点E(-2,- ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com