
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.
已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的![]() ,求y=kx+b的解析式.
,求y=kx+b的解析式.
【答案】(1)7;(2)y=﹣2x+2或y=﹣2x﹣2
【解析】
(1)根据次函数y=kx+b与y=﹣2x+4是“平行一次函数”,据此可得到系数k的值,然后利用已知经过的一点的坐标,即可求出函数的表达式;
(2)求出直线与坐标轴的交点坐标,再根据函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的![]() ,列方程即可求出y=kx+b的解析.
,列方程即可求出y=kx+b的解析.
解:(1)∵一次函数y=kx+b与y=﹣2x+4是“平行一次函数”,
∴k=﹣2,即y=﹣2x+b.
∵函数y=kx+b的图象过点(3,1),
∴1=﹣2×3+b,
∴b=7.
(2)在y=﹣2x+4中,令x=0,得y=4,令y=0,得x=2,
∴A(2,0),B(0,4),
∴S△AOB=![]() OAOB=4.
OAOB=4.
由(1)知k=﹣2,则直线y=﹣2x+b与两坐标轴交点的坐标为(![]() ,0),(0,b),
,0),(0,b),
于是有![]() |b||
|b||![]() |=4×
|=4×![]() =1,
=1,
∴b=±2,
即y=kx+b的解析式为y=﹣2x+2或y=﹣2x﹣2.


科目:初中数学 来源: 题型:
【题目】如图,![]() ,已知
,已知![]() 中,
中,![]() ,
,![]() ,
,![]() 的顶点
的顶点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,当点
上,当点![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在
随之在![]() 上运动,
上运动,![]() 的形状始终保持不变,在运动的过程中,点
的形状始终保持不变,在运动的过程中,点![]() 到点
到点![]() 的最小距离为( )
的最小距离为( )

A. 5 B. 7 C. 12 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
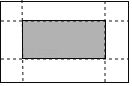
A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣4和y=﹣ax2+4都经过x轴上的A、B两点,两条抛物线的顶点分别为C、D.当四边形ACBD的面积为40时,a的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在总费用2300元的限额内,租用客车送234名学生和6名教师集体外出活动,每辆客车上至少要有1名教师.现有甲、乙两种大客车,它们的载客量和租金如下表所示.
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 45 | 30 |
租金/(元/辆) | 400 | 280 |
(1)共需租多少辆客车?
(2)请给出最节省费用的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假快到了,父母找算带兄妹俩去某个景点旅游一次,长长见识,可哥哥坚持去黄山,妹妹坚持去泰山,争执不下,父母为了公平起见,决定设计一款游戏,若哥哥赢了就去黄山,妹妹赢了就去泰山.下列游戏中,不能选用的是( )
A. 掷一枚硬币,正面向上哥哥赢,反面向上妹妹赢
B. 同时掷两枚硬币,两枚都正面向上,哥哥赢,一正一反向上妹妹赢
C. 掷一枚骰子,向上的一面是奇数则哥哥赢,反之妹妹赢
D. 在不透明的袋子中装有两黑两红四个球,除颜色外,其余均相同,随机摸出一个是黑球则哥哥赢,是红球则妹妹赢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推进青少年毒品预防教育“6·27“工程,切实提高广大青少年识毒、防毒、拒毒的意识和能力,甘肃省各市高度重视全国青少年禁毒知识竞赛活动,强化措施落实,落实工作责任,取得了一定成绩.某市实验中学针对该校九年级学生的知识竞赛成绩绘制了如下不完整的统计图表.

根据所给信息,解答下列问题.
(1)a=__________,b=________.
(2)请求出C组所在扇形统计图中的圆心角的度数.
(3)补全知识竞赛成绩频数分布直方图.
(4)已知该市九年级有3500名学生,请估算全市九年级知识竞赛成绩低于80分的人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com