
【题目】如图,在![]() 中,
中,![]() 、
、![]() 两点分别在边
两点分别在边![]() 、
、![]() 上,
上,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为________.
的面积为________.

【答案】![]()
【解析】
根据等高的两个三角形底边的关系,可得两个三角形面积的关系,根据相似三角形判定与性质,可得AE:EG=AF:FD=3:4,根据比例的性质,可得AF:AD=3:7,再根据等高的两个三角形底边的关系,可得两个三角形面积的关系.
如图,过D作DG∥BE,交AC与G,
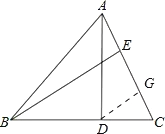
∵AE:EC=CD:BD=1:2,△ABC的面积为21,
∴S△ABE:S△BCE=S△ADC:S△ABD=1:2,
∴S△ABD=![]() S△ABC=
S△ABC=![]() ×21=14,
×21=14,
∵DG∥BE,
∴△CDG∽△CBE,△AEF∽△AGD,
∴![]() =
=![]() =
=![]() ,
,
GE=![]() CE,AE=
CE,AE=![]() CE,
CE,
AE:EG=AF:FD=3:4,
AF:AD=3:7.
S△ABF:S△ABD=3:7,
S△ABF=![]() =
=![]() 37×14=6,
37×14=6,
故答案为:6.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】2008年5月12日,四川省发生8.0级地震,某市派出两个抢险救灾工程队赶到汶川支援,甲工程队承担了2400米道路抢修任务,乙工程队比甲工程队多承担了600米的道路抢修任务,甲工程队施工速度比乙工程队每小时少修40米,结果两工程队同时完成任务.
问甲、乙两工程队每小时各抢修道路多少米.
(1)设乙工程队每小时抢修道路x米,则用含x的式子表示:甲工程队每小时抢修道路 米,甲工程队完成承担的抢修任务所需时间为 小时,乙工程队完成承担的抢修任务所需时间为 小时.
(2)列出方程,完成本题解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,人们对PM2.5 (空气中直径小于等于2.5微米的颗粒)的关注日益密切.我市某天中PM2.5的值y1 (u g/m3) 随时间t (h)的变化如图所示,设y2表示0时,到t时PM2.5的最大值与最小值的差,则y2与t的函数关系大致是 ( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
⑴如图1,若∠BAC=60°,求证:△CEF是等边三角形.
⑵若∠BAC<60°.
①如图2,当点D在线段CB上移动时,判断△CEF为等腰三角形并证明;
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请你在图3中画出相应的图形并直接写出结论(不必证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义![]() 为函数
为函数![]() 的特征数,下面给出特征数为
的特征数,下面给出特征数为![]() 的函数的一些结论:
的函数的一些结论:
①当![]() 时,函数图象的顶点坐标是
时,函数图象的顶点坐标是![]() ;
;
②当![]() 时,函数图象截
时,函数图象截![]() 轴所得的线段长度大于
轴所得的线段长度大于![]() ;
;
③当![]() 时,函数在
时,函数在![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
④当![]() 时,函数图象经过同一个点.
时,函数图象经过同一个点.
其中正确的结论有( )
A. ①②③④ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.
已知函数y=﹣2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=﹣2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的面积是△AOB面积的![]() ,求y=kx+b的解析式.
,求y=kx+b的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com