Question

【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.

⑴如图1,若∠BAC=60°,求证：△CEF是等边三角形.

⑵若∠BAC＜60°.

①如图2,当点D在线段CB上移动时，判断△CEF为等腰三角形并证明;

②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请你在图3中画出相应的图形并直接写出结论(不必证明).

Answer 1

【答案】（1）见解析；（2）①证明见解析；②△CEF为等腰三角形，证明见解析

【解析】

（1）根据题意推出△ABC为等边三角形，然后通过求证△ABD≌△ACE，结合平行线的性质，即可证得结论；

（2）①根据（1）的推理依据，求证△ABD≌△ACE，结合平行线的性质，即可证得结论；

②根据题意画出图形，利用（1）的推理依据，求证△ABD≌△ACE，再利用等角的补角相等，，结合平行线的性质，即可证得结论.

证明：⑴ ∵AB=AC，∠BAC=60

∴△ABC为等边三角形，

在△ABD和△ACE中:

∠BAD=60-∠DAC

∠CAE=60O-∠DAC

∴ ∠BAD=∠CAE

又∵AB=AC，AD=AE

∴△ABD≌△ACE

∴∠ACE= ∠ABD=60

又∵ EF∥BC

∴∠EFC= ∠ACB=60

∴∠FEC=60

∴△CEF是等边三角形

⑵ ①△CEF为等腰三角形，理由如下：

∵AB=AC

∴∠ABC=∠ACB

在△ABD和△ACE中:

∠BAD=∠BAC-∠DAC

∠CAE=∠DAE-∠DAC

而∠DAE=∠BAC

∴ ∠BAD=∠CAE

又∵AB=AC，AD=AE

∴△ABD≌△ACE

∴∠ABC=∠ACE

又∵EF∥BC

∴ ∠EFC= ∠ACB

而∠ABC=∠ACB

∴∠EFC= ∠ECF

所以，△CEF为等腰三角形.

②当点D在线段CB的延长线上时 ，

△CEF为等腰三角形,如图3

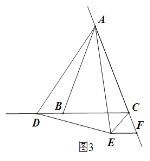
理由如下：

∵AB=AC

∴ ∠ABC=∠ACB

在△ABD和△ACE中:

∠BAD=∠DAE -∠BAE

∠CAE=∠BAC -∠BAE

而∠DAE=∠BAC

∴ ∠BAD=∠CAE

又∵AB=AC，AD=AE

∴△ABD≌△ACE

∴∠ABD=∠ACE

∴∠ABC=∠ECF (等角的补角相等)

又∵EF∥BC

∴∠EFC= ∠ACB

而∠ABC=∠ACB

∴∠EFC= ∠ECF

所以，△CEF为等腰三角形.