
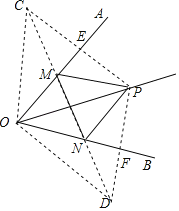
【题目】如图,∠AOB=60°,点M,N分别是射线OA,OB上的动点,OP平分∠AOB,OP=8,当△PMN周长取最小值时,△OMN的面积为_____.

【答案】![]()
【解析】
设点P关于OA的对称点为C,关于OB的对称点为D,当点M、N在CD上时,△PMN的周长最小,然后根据菱形的面积公式即可得到结论.
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PC、PD.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA=30°;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=8,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=120°,∠COP=∠COP=60°,
∴△COP与△POD是等边三角形,
∴四边形OCPD是菱形,
∴CD垂直平分OP,
∴∠PCD=∠PDC=30°,OM=PM,PN=ON,∵∠PCM=∠MPC=30°,
∴∠PMN=60°,
同理∠PNM=60°,
∴PM=PN,
∴四边形PMON是菱形,
∵OP=8,
∴MN=![]() ,
,
∴△OMN的面积=![]() S菱形PMON=
S菱形PMON=![]() ×
×![]() ×8×
×8×![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是一个被平均分成![]() 等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为
等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为![]() ,乙转动转盘后指针所指区域内的数字为
,乙转动转盘后指针所指区域内的数字为![]() (当指针在边界上时,重转一次,直到指向一个区域为止).
(当指针在边界上时,重转一次,直到指向一个区域为止).

![]() 直接写出甲转动转盘后所指区域内的数字为负数的概率;
直接写出甲转动转盘后所指区域内的数字为负数的概率;
![]() 用树状图或列表法,求出点
用树状图或列表法,求出点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,﹣3),B(5,﹣1),C(1,3),结合所给的平面直角坐标系,解答下列问题:

(1)请在如图坐标系中画出△ABC;
(2)画出△ABC关于y轴对称的△A'B'C',并写出△A'B'C'各顶点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
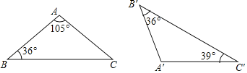
【题目】具备下列各组条件的两个三角形中,不一定相似的是( )
A. 有一个角是![]() 的两个等腰三角形 B. 有一个角为
的两个等腰三角形 B. 有一个角为![]() 的两个等腰三角形
的两个等腰三角形
C. 有一锐角对应相等的两个直角三角形 D. 图中的![]() 与
与![]() 相似
相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为射线CB上一个动点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,过点E作EF∥BC,交直线AC于点F,连接CE.
⑴如图1,若∠BAC=60°,求证:△CEF是等边三角形.
⑵若∠BAC<60°.
①如图2,当点D在线段CB上移动时,判断△CEF为等腰三角形并证明;
②当点D在线段CB的延长线上移动时,△CEF是什么三角形?请你在图3中画出相应的图形并直接写出结论(不必证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;
![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;
![]() ;
;
![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=90°,∠ACB=30°,BC=![]() ,点D在边BC上,连接AD,在AD上方作等边三角形ADE,连接EC.
,点D在边BC上,连接AD,在AD上方作等边三角形ADE,连接EC.
(1)求证:DE=CE;
(2)若点D在BC延长线上,其他条件不变,直接写出DE,CE之间的数量关系(不必证明);
(3)当点D从点B出发沿着线段BC运动到点C时,求点E的运动路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
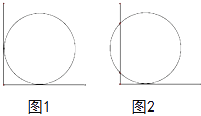
【题目】如图1,把圆形井盖卡在角尺〔角的两边互相垂直,一边有刻度)之间,即圆与两条直角边相切,现将角尺向右平移10cm,如图2,OA边与圆的两个交点对应CD的长为40cm则可知井盖的直径是( )
A. 25cm B. 30cm C. 50cm D. 60cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,直角尺的直角顶点
,直角尺的直角顶点![]() 在
在![]() 上滑动时(点
上滑动时(点![]() 与
与![]() ,
,![]() 不重合),
不重合),

一直角边经过点![]() ,另一直角边
,另一直角边![]() 交于点
交于点![]() ,我们知道,结论“
,我们知道,结论“![]() ”成立.
”成立.
![]() 当
当![]() 时,求
时,求![]() 的长;
的长;
![]() 是否存在这样的点
是否存在这样的点![]() ,使
,使![]() 的周长等于
的周长等于![]() 周长的
周长的![]() 倍?若存在,求出
倍?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com