
【题目】已知二次函数的表达式为![]() .
.
![]() 试判断该二次函数的图象与
试判断该二次函数的图象与![]() 轴交点的个数?并说明理由.
轴交点的个数?并说明理由.
![]() 此二次函数的图象与函数
此二次函数的图象与函数![]() 的图象的一个交点在
的图象的一个交点在![]() 轴上,求
轴上,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
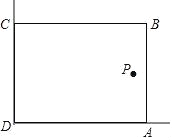
A. 193 B. 194 C. 195 D. 196
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P,满足∠PAB=∠PBC=∠PCA=α,则称点P为△ABC的布洛卡点.通过研究一些特殊三角形中的布洛卡点,得到如下两个结论:
①若∠BAC=90°,则必有∠APC=90°;②若AB=AC,则必有∠APB=∠BPC.
对于这两个结论,下列说法正确的是( )
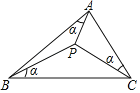
A.①对,②错B.①错,②对C.①,②均错D.①,②均对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,给定∠AOB=60°,及OB边上一点C,如图所示.到射线OA,OB距离相等的所有点组成图形G,线段OC的垂直平分线交图形G于点D,连接CD.
(1)依题意补全图形;直接写出∠DCO的度数;
(2)过点D作OD的垂线,交OA于点E,OB于点F.求证:CF=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,已知
,已知![]() 中,
中,![]() ,
,![]() ,
,![]() 的顶点
的顶点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,当点
上,当点![]() 在边
在边![]() 上运动时,
上运动时,![]() 随之在
随之在![]() 上运动,
上运动,![]() 的形状始终保持不变,在运动的过程中,点
的形状始终保持不变,在运动的过程中,点![]() 到点
到点![]() 的最小距离为( )
的最小距离为( )

A. 5 B. 7 C. 12 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )
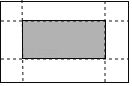
A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com