
如图,在△ABC中,AB=5,BC=3,AC=4,动点E(与点A、C不重合)在AC边上,EF∥AB交BC于点F.
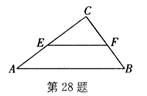
1.当△ECF的面积与四边形EABF的面积相等时,求CE的长
2.当△ECF的周长与四边形EABF的周长相等时,求CE的长
3.试问在AB上是否存在点P,使得△EFP为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出EF的长.
1.CE=2![]()
2.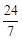
3.在AB上存在点P.使△EFP为等腰直角三角形,此时EF=![]() 或EF=
或EF=![]()
解析:解:(1)∵△ECF的面积与四边形EABF的面积相等,
∴S△ECF:S△ACB=1:2,
又∵EF∥AB,∴△ECF∽△ACB,
∴![]() ,且AC=4,
,且AC=4,
∴CE=2![]() ;
;
(2)设CE的长为x,
∵△ECF∽△ACB,
∴![]() ,∴CF=
,∴CF=![]() x,
x,
由△ECF的周长与四边形EABF的周长相等,得:
x+EF+![]() x=(4-x)+5+(3-
x=(4-x)+5+(3-![]() x)+EF
x)+EF
解得x=![]() ,∴CE的长为
,∴CE的长为![]()
(3)△EFP为等腰直角三角形,有两种情况:
①如图1,假设∠PEF=90°,EP=EF
由AB=5,BC=3,AC=4,得∠C=90°
∴Rt△ACB斜边AB上高CD=![]() ,设EP=EF=x,由△ECF∽△ACB,得:
,设EP=EF=x,由△ECF∽△ACB,得:
![]()
即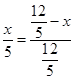 ,
,
解得x=![]() ,即EF=
,即EF=![]()
当∠EFP´=90°,EF=FP′时,同理可得EF=![]() ;
;
②如图2,假设∠EPF=90°,PE=PF时,点P到EF的距离为![]() EF
EF
设EF=x,由△ECF∽△ACB,得:
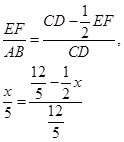
解得x=![]() ,即EF=
,即EF=![]()
综上所述,在AB上存在点P,使△EFP为等腰直角三角形,此时EF=![]() 或EF=
或EF=![]()


科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com