
| 2 |
202+(40
|
| n•π•60 |
| 180 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
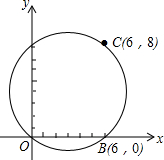 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由这三个观测点确定的圆形区域是海洋生物保护区.查看答案和解析>>
科目:初中数学 来源: 题型:
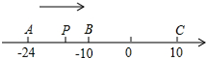 已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
已知数轴上有A、B、C三个点,分别表示有理数-24,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )| A、30° | B、36° |
| C、50° | D、60° |
查看答案和解析>>
科目:初中数学 来源: 题型:
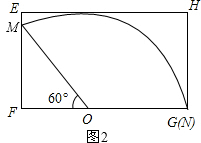
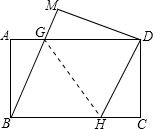 如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( )
如图,在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿GH折叠,使点B与D重合,则下列语句正确的是( )| A、只有①② | B、只有②③ |
| C、①②③ | D、①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com