【题目】在我市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元.

（1）求每台电脑、每台电子白板各多少万元?

（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，该校有几种购买方案？

（3）上面的哪种方案费用最低？按费用最低方案购买需要多少钱？

参考答案：

【答案】（1）每台电脑0.5万元，每台电子白板1.5万元；（2）方案一：购进电脑15台，电子白板15台；方案二：购进电脑16台，电子白板14台，方案三：购进电脑17台，电子白板13台；（3）选择方案三最省钱，即购买电脑17台，电子白板13台最省钱．需要28万元．

【解析】试题分析：（1）先设每台电脑x万元，每台电子白板y万元，根据购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元列出方程组，求出x，y的值即可；

（2）先设需购进电脑a台，则购进电子白板（30-a）台，根据需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元列出不等式组，求出a的取值范围，再根据a只能取整数，得出购买方案；

（3）根据每台电脑的价格和每台电子白板的价格，算出总费用，再进行比较，即可得出最省钱的方案．

试题解析：（1）设每台电脑x万元，每台电子白板y万元，根据题意得：

解得：

答：每台电脑0.5万元，每台电子白板1.5万元.

（2）设需购进电脑a台，则购进电子白板（30-a）台，

则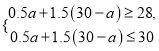

解得：15≤a≤17，即a=15、16、17．

故共有三种方案：

方案一：购进电脑15台，电子白板15台；

方案二：购进电脑16台，电子白板14台；

方案三：购进电脑17台，电子白板13台.

(3) 方案一：总费用为万元；

方案二：总费用为万元；

方案三：总费用为万元；

所以，方案三费用最低，需28万元.

关闭