

分析 (1)直接利用苹果和香蕉的采购单价分别为4元/千克和3元/千克,进而表示出总价得出等式即可;
(2)利用香蕉的价格为5元/千克,且这两种水果的重量都正常损耗10%,分别表示出其利润得出不等式求出答案.
解答 解:(1)设采购人员购买了苹果x千克,香蕉(1100-x)千克,由题意可得:
4x-3(1100-x)=4000,
解得:x=700,
1100-x=1100-700=400,
答:采购人员购买了苹果700千克,香蕉400千克;
(2)设苹果售价至少应定为每千克y元,由题意可得:
700×(1-0.1)y+400×(1-0.1)×5-4000≥4000×39.5%,
解得:y≥6,
答:苹果售价至少应定为每千克6元.
点评 此题主要考查了一元一次不等式的应用以及一元一次方程的应用,正确表示出香蕉与苹果的利润是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
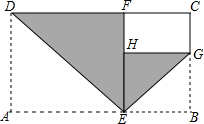 如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处.
如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
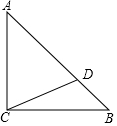 如图,在△ABC中,∠ACB=90°,AC=BC=AD
如图,在△ABC中,∠ACB=90°,AC=BC=AD查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com