
����Ŀ����ͼ����Rt��ABC�У���ABC=90�㣮AB=BC����D���߶�AB�ϵ�һ�㣬����CD������B��BG��CD���ֱ�CD��CA�ڵ�E��F�������A�Ҵ�ֱ��AB��ֱ���ཻ�ڵ�G������DF�����������ĸ����ۣ��� ![]() =
= ![]() ��������D��AB���е㣬��AF=
��������D��AB���е㣬��AF= ![]() AB���۵�B��C��F��D�ĵ���ͬһ��Բ��ʱ��DF=DB������
AB���۵�B��C��F��D�ĵ���ͬһ��Բ��ʱ��DF=DB������ ![]() =
= ![]() ����S��ABC=9S��BDF �� ������ȷ�Ľ�������ǣ� ��
����S��ABC=9S��BDF �� ������ȷ�Ľ�������ǣ� ��
A.�٢�
B.�ۢ�
C.�٢ڢ�
D.�٢ڢۢ�
���𰸡�C
���������⣺������ɵ�BC��AG��
���AFG�ס�BFC��
�� ![]() ��
��
��AB=BC���� ![]() ��
��
�ʽ��ۢ���ȷ��
����ͼ���ߡ�1+��3=90�㣬��1+��4=90�㣬
���3=��4��
�ڡ�ABG���BCD�У�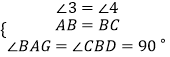 ��
��
���ABG�ա�BCD��ASA����
��AG=BD����BD=AD��
��AG=AD��
�ڡ�AFG���AFD�У� 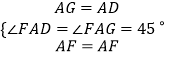 ��
��
���AFG�ա�AFD��SAS��
�ߡ�ABCΪ����ֱ�������Σ���AC= ![]() AB��
AB��
�ߡ�AFG�ա�AFD����AG=AD= ![]() AB=
AB= ![]() BC��
BC��
�ߡ�AFG�ס�BFC���� ![]() =
= ![]() ����FC=2AF��
����FC=2AF��
��AF= ![]() AC=
AC= ![]() AB��
AB��
�ʽ��ۢ���ȷ��
��B��C��F��D�ĵ���ͬһ��Բ��ʱ��
���2=��ACB
�ߡ�ABC=90�㣬AB=BC��
���ACB=��CAB=45�㣬
���2=45�㣬
���CFD=��AFD=90�㣬
��CD��B��C��F��D�ĵ�����Բ��ֱ����
��BG��CD��
�� ![]() ��
��
��DF=DB���ʢ���ȷ��
�� ![]() ����AG=BD��
����AG=BD�� ![]() ��
��
�� ![]() ����
���� ![]() =
= ![]() ����AF=
����AF= ![]() AC����S��ABF=
AC����S��ABF= ![]() S��ABC����S��BDF=
S��ABC����S��BDF= ![]() S��ABF ��
S��ABF ��
��S��BDF= ![]() S��ABC �� ��S��ABC=12S��BDF ��
S��ABC �� ��S��ABC=12S��BDF ��
�ʽ��ܴۢ���
��ѡC��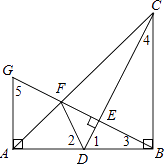
�����㾫�������ڱ��⿼��Ľ�ֱ�������Σ���Ҫ�˽���ֱ�������ε����ݣ��ٱߵĹ�ϵa2+b2=c2���ڽǵĹ�ϵ��A+B=90�㣻�۱߽ǹ�ϵ�����Ǻ��Ķ��壮(ע�⣺��������ʹ���м����ݺͳ���)���ܵó���ȷ�𰸣�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��������DEFG�У���G��CD�ϣ�DE=2����������DEFG�Ƶ�D˳ʱ����ת60�㣬�õ�������DE��F��G�䣬��ʱ��G����AC�ϣ�����CE�䣬��CE��+CG��=�� �� 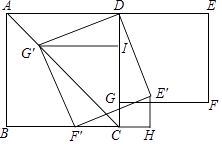
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+4��a��0����x�ύ�ڵ�A�͵�B��2��0������y�ύ�ڵ�C����D���������ڵ�һ���ĵ㣮
��1������ABD�����Ϊ4ʱ��
�����D�����ꣻ
������OD����M���������ϵĵ㣬�ҡ�MDO=��BOD�����M�����ꣻ
��2��ֱ��BD��AD�ֱ���y�ύ�ڵ�E��F����ôOE+OF��ֵ�Ƿ�仯����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�Ƿ���������y= ![]() ����0����ͼ��������һ�㣬AB��x�ύ����������y=��
����0����ͼ��������һ�㣬AB��x�ύ����������y=�� ![]() ��ͼ���ڵ�B����ABΪ����ƽ���ı���ABCD������C��D��x���ϣ���ƽ���ı���ABCD�����Ϊ�� ��
��ͼ���ڵ�B����ABΪ����ƽ���ı���ABCD������C��D��x���ϣ���ƽ���ı���ABCD�����Ϊ�� �� 
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ǡ�ABC�У�D��E�ֱ�ΪAB��BC�е㣬FΪAC��һ�㣬�ҡ�AFE=��A��DM��EF��AC�ڵ�M�� 
��1����G��BE�ϣ��ҡ�BDG=��C����֤��DGCF=DMEG��
��2����ͼ�У�ȡCE��һ��H��ʹ��CFH=��B����BG=1����EH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��ԲO��ֱ����AB��AD��ԲO���ң���AB=AD������BC��DC�� 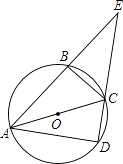
��1����֤����ABC�ա�ADC��
��2���ӳ�AB��DC���ڵ�E����EC=5cm��BC=3cm�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������x�ύ��A����1��0����E��3��0�����㣬��y�ύ�ڵ�B��0��3����
��1���������ߵĽ���ʽ��
��2���������߶���ΪD�����ı���AEDB�������
��3����AOB���DBE�Ƿ����ƣ�������ƣ������֤������������ƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڸոձ�Ļ��2016ȫ�������ᡱ������������Ȼ����ό�㣬ij�м���Ϊ���˽���նԡ������������⡱�ľ۽��㣬��������˲��������Ե�����������������������ͼ��ʾ��ͳ��ͼ�������������� 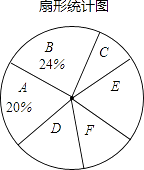
�l���ֲ���
��� | ���㻰�� | Ƶ���������� |
A | ҽ������ | 100 |
B | ʳƷ��ȫ | m |
C | ����ס�� | 40 |
D | ��ᱣ�� | 80 |
E | ��̬���� | n |
F | ���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺
��1����գ�m= �� n= �� ����ͳ��ͼ��E�飬F����ռ�İٷֱȷֱ�Ϊ��
��2�����������˿ڴ�Լ800������������й�עB�黰���������
��3��������ν��ܵ���������У�������һ�ˣ�����˹�עA�黰��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com