Question

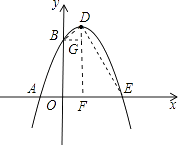
【题目】如图，已知抛物线与x轴交于A（﹣1，0）、E（3，0）两点，与y轴交于点B（0，3）．

（1）求抛物线的解析式；
（2）设抛物线顶点为D，求四边形AEDB的面积；
（3）△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由．

Answer 1

【答案】
（1）

解：∵抛物线与y轴交于点（0，3），

∴设抛物线解析式为y=ax2+bx+3（a≠0）

根据题意，得 ，

解得 ．

∴抛物线的解析式为y=﹣x2+2x+3

（2）

解：如图，设该抛物线对称轴是DF，连接DE、BD．过点B作BG⊥DF于点G．

由顶点坐标公式得顶点坐标为D（1，4）

设对称轴与x轴的交点为F

∴四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE

= AOBO+ （BO+DF）OF+ EFDF

= ×1×3+ ×（3+4）×1+ ×2×4

=9

（3）

解：相似，如图，

BD= ；

∴BE=

DE=

∴BD2+BE2=20，DE2=20

即：BD2+BE2=DE2，

所以△BDE是直角三角形

∴∠AOB=∠DBE=90°，且 ，

∴△AOB∽△DBE．

【解析】（1）易得c=3，故设抛物线解析式为y=ax2+bx+3，根据抛物线所过的三点的坐标，可得方程组，解可得a、b的值，即可得解析式；（2）易由顶点坐标公式得顶点坐标，根据图形间的关系可得四边形ABDE的面积=S△ABO+S梯形BOFD+S△DFE ， 代入数值可得答案；（3）根据题意，易得∠AOB=∠DBE=90°，且 ，即可判断出两三角形相似．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．