
【题目】下列几何体的主视图既是中心对称图形又是轴对称图形的是( )
A.
B.
C.
D.
【答案】D
【解析】解:A、主视图是等腰三角形,是轴对称图形,不是中心对称图形,故错误; B、主视图是等腰三角形,是轴对称图形,不是中心对称图形,故错误;
C、主视图是等腰梯形,是轴对称图形,不是中心对称图形,故错误;
D、主视图是矩形,是轴对称图形,也是中心对称图形,故正确.
故选:D.
【考点精析】本题主要考查了轴对称图形和常见几何体的三视图的相关知识点,需要掌握两个完全一样的图形关于某条直线对折,如果两边能够完全重合,我们就说这两个图形成轴对称,这条直线就对称轴;俯视图放在主视图的下面,长度与主视图的长度一样;左视图放在主视图的右面,高度与主视图的高度一样,宽度与俯视图的宽度一样,可简记为“长对正;高平齐;宽相等”才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元. 设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 | 2 | … | ||
乙复印店收费(元) | 0.6 | 2.4 | … |
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1 , y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.
(1)当△ABD的面积为4时,
①求点D的坐标;
②联结OD,点M是抛物线上的点,且∠MDO=∠BOD,求点M的坐标;
(2)直线BD、AD分别与y轴交于点E、F,那么OE+OF的值是否变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M. 
(1)点G在BE上,且∠BDG=∠C,求证:DGCF=DMEG;
(2)在图中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是圆O的直径,AB、AD是圆O的弦,且AB=AD,连结BC、DC. 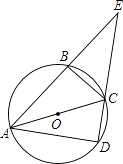
(1)求证:△ABC≌△ADC;
(2)延长AB、DC交于点E,若EC=5cm,BC=3cm,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).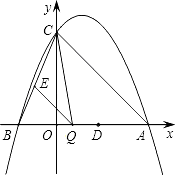
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com