
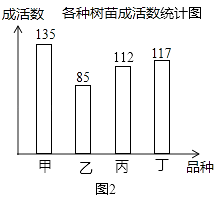
����Ŀ��ij�н���ɭ�ֳ�����Ҫ���������磬ij��̬ʾ������Լס��ҡ��������ĸ�Ʒ�ֵ����繲500���������ɻ������飬����ѡ��ɻ��ʸߵ�Ʒ�ֽ����ƹ㣮ͨ��ʵ���֪����������ijɻ���Ϊ89.6%����ʵ�����ݻ��Ƴ���������ͳ��ͼ��������Ϣδ�������� 
��1��ʵ�����õ�����������������꣮
��2�������������ijɻ���������ͼ2����������
��3������ΪӦѡ������������ƹ㣿
��4����ͨ������˵�����ɣ�
���𰸡�
��1��100
��2���⣺500��25%��89.6%=112���꣩��
��ȫͳ��ͼ��ͼ
��3���⣺Ӧѡ����Ʒ�ֽ����ƹ�
��4���⣺��������ɻ���Ϊ�� ![]() ��100%=90%��
��100%=90%��
���ֹ�����ɻ���Ϊ�� ![]() ��100%=85%��
��100%=85%��
���ֹ�����ɻ���Ϊ�� ![]() ��100%=93.6%��
��100%=93.6%��
��93.6%��90%��89.6%��85%��
��Ӧѡ����Ʒ�ֽ����ƹ㣬���ijɻ�����ߣ�Ϊ93.6%
���������⣺��1��500����1��25%��25%��30%��=100���꣩�� ���Դ���100��
�����㾫������������ͳ��ͼ������ͳ��ͼ�ǽ����ĸ�������Ҫ֪��������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC��ԲO��ֱ����AB��AD��ԲO���ң���AB=AD������BC��DC�� 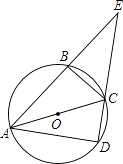
��1����֤����ABC�ա�ADC��
��2���ӳ�AB��DC���ڵ�E����EC=5cm��BC=3cm�����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������x�ύ��A����1��0����E��3��0�����㣬��y�ύ�ڵ�B��0��3����
��1���������ߵĽ���ʽ��
��2���������߶���ΪD�����ı���AEDB�������
��3����AOB���DBE�Ƿ����ƣ�������ƣ������֤������������ƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�BCE�У���A�DZ�BE��һ�㣬��ABΪֱ���ġ�O��CE�����ڵ�D��AD��OC����FΪOC���O�Ľ��㣬����AF�� 
��1����֤��CB�ǡ�O�����ߣ�
��2������ECB=60�㣬AB=6����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������y=ax2��2ax+c��a��0����y�ύ�ڵ�C��0��4������x�ύ�ڵ�A��B����A������Ϊ��4��0����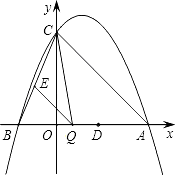
��1����������ߵĽ���ʽ��
��2����Q���߶�AB�ϵĶ��㣬����Q��QE��AC����BC�ڵ�E������CQ������CQE��������ʱ�����Q�����ꣻ
��3����ƽ����x��Ķ�ֱ��l��������߽��ڵ�P����ֱ��AC���ڵ�F����D������Ϊ��2��0�����ʣ��Ƿ����������ֱ��l��ʹ�á�ODF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ����������P1��x1 �� y1����P2��x2 �� y2������|x1��x2|+|y1��y2|ΪP1��P2�����ֱ�Ǿ��룬������d��P1 �� P2����P0��2����3����һ���㣬Q��x��y����ֱ��y=kx+b�ϵ�һ���㣬��d��P0 �� Q������СֵΪP0��ֱ��y=kx+b��ֱ�Ǿ��룮��P��a����3����ֱ��y=x+1��ֱ�Ǿ���Ϊ6����a= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڸոձ�Ļ��2016ȫ�������ᡱ������������Ȼ����ό�㣬ij�м���Ϊ���˽���նԡ������������⡱�ľ۽��㣬��������˲��������Ե�����������������������ͼ��ʾ��ͳ��ͼ�������������� 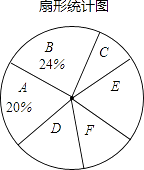
�l���ֲ���
��� | ���㻰�� | Ƶ���������� |
A | ҽ������ | 100 |
B | ʳƷ��ȫ | m |
C | ����ס�� | 40 |
D | ��ᱣ�� | 80 |
E | ��̬���� | n |
F | ���� | 60 |
�����ͼ�����ṩ����Ϣ����������⣺
��1����գ�m= �� n= �� ����ͳ��ͼ��E�飬F����ռ�İٷֱȷֱ�Ϊ��
��2�����������˿ڴ�Լ800������������й�עB�黰���������
��3��������ν��ܵ���������У�������һ�ˣ�����˹�עA�黰��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��ѡ��ѧ���μӡ�������д���������Ծ��꼶һ�ࡢ�����10��ѧ�����к�����д���ԣ��Ʒֲ���10���ƣ��÷־�ȡ���������ɼ��ﵽ6�ֻ�6������Ϊ���õ�9��Ϊ���㣬�ɼ����1��ʾ���������˳ɼ�����������2����
��1
һ�� | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
���� | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
��2
�༶ | ƽ���� | ��λ�� | ���� | ���� | ������ | ������ |
һ�� | 7.6 | 8 | a | 3.82 | 70% | 30% |
���� | b | 7.5 | 10 | 4.94 | 80% | 40% |
��1���ڱ�2�У�a= ��b= ��
��2������˵����ļ����ʡ������ʾ�����һ�࣬���Զ����һ��ã���Ҳ������Ϊһ��ɼ��ȶ���ã�����������һ��ɼ��õ��������ɣ�
��3��һ�ࡢ��������ֵ���ͬѧ�Ա�ֱ���1��1Ů��2��1Ů���ִ�����������ֵ�ͬѧ�и���1��ͬѧ�μӡ�������д������������״ͼ���б������ǡ�ó鵽1��1Ů��λͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com