
【题目】某地政府计划为农户购买农机设备提供补贴.其中购买Ⅰ型、Ⅱ型设备农民所投资的金额与政府补贴的额度存在下表所示的函数对应关系.
型号 | Ⅰ型设备 | Ⅱ型设备 | |||
投资金额x(万元) | x | 5 | x | 2 | 4 |
补贴金额y(万元) | y1=kx(k≠0) | 2 | y2=ax2+bx(a≠0) | 2.8 | 4 |
(1)分别求y1和y2的函数解析式;
(2)有一农户共投资10万元购买Ⅰ型、Ⅱ型两种设备,两种设备的投资均为整数万元,要想获得最大补贴金额,应该如何购买?能获得的最大补贴金额为多少?
【答案】
(1)
解:设购买Ⅰ型设备补贴的金额的解析式为:y1=kx,购买Ⅱ型设备补贴的金额的解析式为y2=ax2+bx,
由题意,得:2=5k,或 ![]() ,
,
解得:k= ![]() ,
, 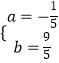 ,
,
∴y1的解析式为:y1= ![]() x,y2的函数解析式为:y2=﹣
x,y2的函数解析式为:y2=﹣ ![]() x2+
x2+ ![]() x
x
(2)
解:设投资Ⅱ型设备a万元,Ⅰ型设备(10﹣a)万元,补贴金额为W万元:
所以W=y1+y2= ![]() (10﹣a)+(﹣
(10﹣a)+(﹣ ![]() a2+
a2+ ![]() a)
a)
=﹣ ![]() (a﹣
(a﹣ ![]() )2+
)2+ ![]()
所以当a=3或4时,W的最大值= ![]() ,所
,所
以投资Ⅰ型设备7万元,Ⅱ型设备3万元;或投资Ⅰ型设备6万元,Ⅱ型设备4万元,获得最大补贴金额,最大补贴金额为 ![]() 万元
万元
【解析】(1)利用待定系数法直接就可以求出y1与y2的解析式.(2)设总补贴金额为W万元,购买Ⅱ型设备a万元,购买Ⅰ型设备(10﹣a)万元,建立等式就可以求出其值.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.
(1)当△ABD的面积为4时,
①求点D的坐标;
②联结OD,点M是抛物线上的点,且∠MDO=∠BOD,求点M的坐标;
(2)直线BD、AD分别与y轴交于点E、F,那么OE+OF的值是否变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).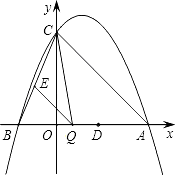
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中任意两点P1(x1 , y1)、P2(x2 , y2),称|x1﹣x2|+|y1﹣y2|为P1、P2两点的直角距离,记作:d(P1 , P2).P0(2,﹣3)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P0 , Q)的最小值为P0到直线y=kx+b的直角距离.若P(a,﹣3)到直线y=x+1的直角距离为6,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,若∠BAC=80°,∠C=50°,取AC中点P,连接PO并延长交BC于点M,连接AM,则∠BAM=( ) 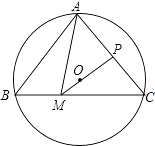
A.45°
B.30°
C.50°
D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在刚刚闭幕的2016全国“两会”,民生话题依然是社会焦点,某市记者为了了解百姓对“两会民生话题”的聚焦点,随机调查了部分市民,并对调查结果进行整理.绘制了如图所示的统计图表(不完整). 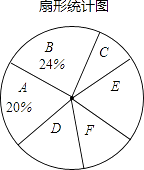
頻数分布表
组别 | 焦点话题 | 频数(人数) |
A | 医疗卫生 | 100 |
B | 食品安全 | m |
C | 教育住房 | 40 |
D | 社会保障 | 80 |
E | 生态环境 | n |
F | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= , n= . 扇形统计图中E组,F组所占的百分比分别为、
(2)该市现有人口大约800万,请你估计其中关注B组话题的人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注A组话题的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
(1)从运动开始,当t取何值时,PQ∥CD?
(2)从运动开始,当t取何值时,△PQC为直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com