
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N. 
(1)求证:CA=CN;
(2)连接DF,若cos∠DFA= ![]() ,AN=2
,AN=2 ![]() ,求圆O的直径的长度.
,求圆O的直径的长度.
【答案】
(1)证明:连接OF,则∠OAF=∠OFA,如图所示.
∵ME与⊙O相切,
∴OF⊥ME.
∵CD⊥AB,
∴∠M+∠FOH=180°.
∵∠BOF=∠OAF+∠OFA=2∠OAF,∠FOH+∠BOF=180°,
∴∠M=2∠OAF.
∵ME∥AC,
∴∠M=∠C=2∠OAF.
∵CD⊥AB,
∴∠ANC+∠OAF=∠BAC+∠C=90°,
∴∠ANC=90°﹣∠OAF,∠BAC=90°﹣∠C=90°﹣2∠OAF,
∴∠CAN=∠OAF+∠BAC=90°﹣∠OAF=∠ANC,
∴CA=CN.

(2)连接OC,如图2所示.
∵cos∠DFA= ![]() ,∠DFA=∠ACH,
,∠DFA=∠ACH,
∴ ![]() =
= ![]() .
.
设CH=4a,则AC=5a,AH=3a,
∵CA=CN,
∴NH=a,
∴AN= ![]() =
= ![]() =
= ![]() a=2
a=2 ![]() ,
,
∴a=2,AH=3a=6,CH=4a=8.
设圆的半径为r,则OH=r﹣6,
在Rt△OCH中,OC=r,CH=8,OH=r﹣6,
∴OC2=CH2+OH2,r2=82+(r﹣6)2,
解得:r= ![]() ,
,
∴圆O的直径的长度为2r= ![]() .
.

【解析】(1)连接OF,根据切线的性质结合四边形内角和为360°,即可得出∠M+∠FOH=180°,由三角形外角结合平行线的性质即可得出∠M=∠C=2∠OAF,再通过互余利用角的计算即可得出∠CAN=90°﹣∠OAF=∠ANC,由此即可证出CA=CN;(2)连接OC,由圆周角定理结合cos∠DFA= ![]() 、AN=2
、AN=2 ![]() ,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
,即可求出CH、AH的长度,设圆的半径为r,则OH=r﹣6,根据勾股定理即可得出关于r的一元一次方程,解之即可得出r,再乘以2即可求出圆O直径的长度.
【考点精析】根据题目的已知条件,利用勾股定理的概念和圆周角定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了解高邮市6000名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分30分,得分均为整数),制成下表:
分数段(x分) | x≤10 | 11≤x≤15 | 16≤x≤20 | 21≤x≤25 | 26≤x≤30 |
人 数 | 10 | 15 | 35 | 112 | 128 |
(1)本次抽样调查共抽取了名学生;
(2)若用扇形统计图表示统计结果,则分数段为x≤10的人数所对应扇形的圆心角为°;
(3)学生英语口语考试成绩的众数落在11≤x≤15的分数段内;(填“会”或“不会”)
(4)若将26分以上(含26)定为优秀,请估计该区九年级考生成绩为优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( ) 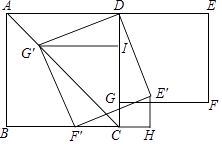
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A4纸复印文件,在甲复印店不管一次复印多少页,每页收费0.1元.在乙复印店复印同样的文件,一次复印页数不超过20时,每页收费0.12元;一次复印页数超过20时,超过部分每页收费0.09元. 设在同一家复印店一次复印文件的页数为x(x为非负整数).
(1)根据题意,填写下表:
一次复印页数(页) | 5 | 10 | 20 | 30 | … |
甲复印店收费(元) | 0.5 | 2 | … | ||
乙复印店收费(元) | 0.6 | 2.4 | … |
(2)设在甲复印店复印收费y1元,在乙复印店复印收费y2元,分别写出y1 , y2关于x的函数关系式;
(3)当x>70时,顾客在哪家复印店复印花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM= ![]() AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是
AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是 ![]() ,则
,则 ![]() 的值是 .
的值是 . 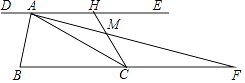
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+4(a≠0)与x轴交于点A和点B(2,0),与y轴交于点C,点D是抛物线在第一象限的点.
(1)当△ABD的面积为4时,
①求点D的坐标;
②联结OD,点M是抛物线上的点,且∠MDO=∠BOD,求点M的坐标;
(2)直线BD、AD分别与y轴交于点E、F,那么OE+OF的值是否变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、E(3,0)两点,与y轴交于点B(0,3).
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com