
分析 (1)根据题目中的式子,可以计算出其结果,注意要化到最简;
(2)根据题目中的信息可以计算出所求式子的结果.
解答 解:(1)-$\frac{1}{4}$×$\frac{1}{5}$=-$\frac{1}{20}$,-$\frac{1}{n}$•$\frac{1}{n+1}$=$-\frac{1}{n(n+1)}$,
故答案为:$-\frac{1}{20}$,$-\frac{1}{n(n+1)}$;
(2)(-1×$\frac{1}{2}$)+(-$\frac{1}{2}$×$\frac{1}{3}$)+(-$\frac{1}{3}$×$\frac{1}{4}$)+…+(-$\frac{1}{2015}$×$\frac{1}{2016}$)
=-1+$\frac{1}{2}+(-\frac{1}{2})+\frac{1}{3}+(-\frac{1}{3})+\frac{1}{4}+…+(-\frac{1}{2015})+\frac{1}{2016}$
=-1+$\frac{1}{2016}$
=-$\frac{2015}{2016}$.
点评 本题考查规律性:数字的变化类,解题的关键是明确题意,找出所求式子中数的变化的特点.


科目:初中数学 来源: 题型:解答题
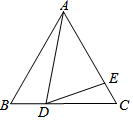 如图,在等边△ABC中,点D是BC边上一动点,且∠ADE=60°,
如图,在等边△ABC中,点D是BC边上一动点,且∠ADE=60°,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片使点A落在边BC上的A'处,折痕为PQ.当点A'在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点B与点A'间的最小距离为1.
在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片使点A落在边BC上的A'处,折痕为PQ.当点A'在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点B与点A'间的最小距离为1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$>$\frac{1}{2}$ | B. | -$\frac{1}{2}$>-$\frac{1}{3}$ | C. | -0.1>-(-0.01) | D. | -4<-3.14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com