
如图,某一次函数y=kx+b的图象与一个反比例函数的图象交于A、B两点,点A和点B关于直线y=x对称.
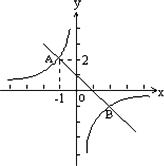
(1)求出这个反比例函数的解析式;
(2)直接写出点B的坐标;
(3)求k和b的值.
科目:初中数学 来源:2012年重庆市北碚区中考适应性考试数学试卷(带解析) 题型:解答题
受国际炒家炒作的影响,今年棉花价格出现了大幅度波动.1至3月份,棉价大幅度上涨,其价格y1 (元/吨)与月份x 之间的函数关系式为:y1=2200x+24200(1≤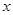 ≤3,且
≤3,且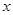 取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份
取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份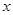 (4≤x≤6,且x取整数)之间的函数关系如图所示.
(4≤x≤6,且x取整数)之间的函数关系如图所示.
(1)直接写出棉价y2 (元/吨)与月份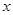 之间所满足的一次函数关系式;
之间所满足的一次函数关系式;
(2)某棉被厂今年1至3月份的棉花进货量p1 (吨)与月份x之间所满足的函数关系式为:p1=-10x+170 (1≤x≤3,且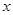 取整数);4至6月份棉花进货量p2(吨)与月份
取整数);4至6月份棉花进货量p2(吨)与月份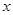 之间所满足的函数关系式为p2=40x-20 (4≤
之间所满足的函数关系式为p2=40x-20 (4≤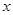 ≤6,且
≤6,且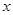 取整数).求在前6个月中该棉被厂的棉花进货金额最大的月份和该月的进货金额;
取整数).求在前6个月中该棉被厂的棉花进货金额最大的月份和该月的进货金额;
(3)经厂方研究决定,若7月份棉价继续下降,则对棉花进行收储.若棉价在6月份的基础上下降a%,则该厂7月份进货量在6月份的基础上增加2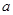 %.若要使7月份进货金额为5130400元,请你估算出
%.若要使7月份进货金额为5130400元,请你估算出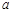 的最大整数值.
的最大整数值.
(参考数据:352=1225,362=1296,372=1369,382=1444)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年山东诸城龙源学校九年级下学期第一次学情检测数学试卷(解析版) 题型:解答题
某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一次函数.

(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式.当销售单价为何值时,所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源:2014届江苏省江都市八年级下学期期中考试数学试卷(解析版) 题型:解答题
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量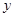 (万件)与销售单位
(万件)与销售单位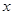 (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
(1)求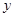 关于
关于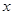 的函数关系式;
的函数关系式;
(2)试写出该公司销售该种产品的年获利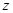 (万元)关于销售单价
(万元)关于销售单价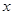 (元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价
(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价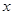 为何值时,年获利最大?并求这个最大值;
为何值时,年获利最大?并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源:2012年沪科版初中数学九年级上23.5二次函数的应用练习卷(解析版) 题型:解答题
某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量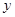 (万件)与销售单位
(万件)与销售单位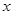 (元)之间存在着如图所示的一次函数关系.
(元)之间存在着如图所示的一次函数关系.
(1)求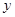 关于
关于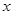 的函数关系式;
的函数关系式;
(2)试写出该公司销售该种产品的年获利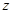 (万元)关于销售单价
(万元)关于销售单价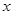 (元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价
(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价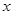 为何值时,年获利最大?并求这个最大值;
为何值时,年获利最大?并求这个最大值;
(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com