
如图,四边形OABC的边OA、OC分别在x轴、y轴上,点5的坐标为(3,2).点D、E分别在AB、BC边上,BD=BE=1.沿直线DE将△BDE翻折,点B落在点B′处.则点B′的坐标为________.
解:∵四边形OABC是矩形,
∴∠B=90°,
∵BD=BE=1,
∴∠BED=∠BDE=45°,
∵沿直线DE将△BDE翻折,点B落在点B′处,
∴∠B′ED=∠BED=45°,∠B′DE=∠BDE=45°,B′E=BE=1,B′D=BD=1,
∴∠BEB′=∠BDB′=90°,
∵点B的坐标为(3,2),
∴点B′的坐标为(2,1).
故答案为:(2,1).
由四边形OABC是矩形,BE=BD=1,易得△BED是等腰直角三角形,由折叠的性质,易得∠BEB′=∠BDB′=90°,又由点B的坐标为(3,2),即可求得点B′的坐标.
题目来源:同步导学案课时练八年级数学上册人教版 > 路径最短


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
1、 如图,在△ABC中,BC=10 ,BD=8,DE⊥BC 于点E,且E为线段BC的中点,则△BCD的周长为( )
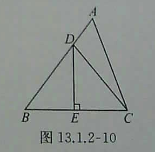
A、20 B、18 C、26 D、28
查看答案和解析>>
科目:初中数学 来源: 题型:
以下运算正确的是()
A、c+c^3=c^4
B、c.c^3=c^4
C、(-3)^4 x(-3)^3=3^7
D、(x-y)(x-y)^2 (x-y)^3(x-y)^5=(x-y)^10
查看答案和解析>>
科目:初中数学 来源: 题型:
3、(a+b)^3.(a+b)^7= ( )
A、(a+b)^21 B、(a+b)^10 C、(a^3+b^3)(a^7+b^7) D、a^10+b^10
查看答案和解析>>
科目:初中数学 来源: 题型:
 ......
......查看答案和解析>>
科目:初中数学 来源: 题型:
如图(1),抛物线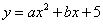 (
(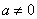 )与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为
)与x轴交于A、B两点,与y轴交于点C,直线AC的解析式为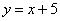 ,抛物线的对称轴与
,抛物线的对称轴与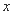 轴交于点E,点D(-2,-3)在对称轴上.
轴交于点E,点D(-2,-3)在对称轴上.
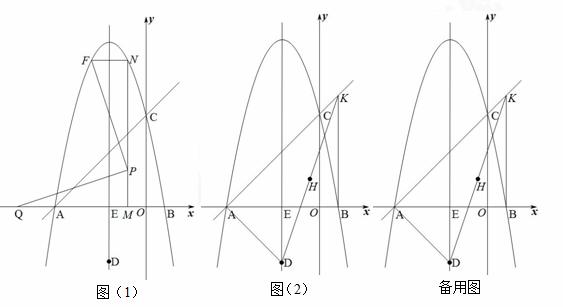
(1)求此抛物线的解析式;
(2)如图(1),若点M是线段OE上一点(点M不与点O、E重合),过点M作MN⊥x轴,交抛物线于点N,记点N关于抛物线对称轴的对称点为点F,点P是线段MN上一点,且满足MN=4MP,连接FN、FP,作QP⊥PF交x轴于点Q,且满足PF=PQ,求点Q的坐标;
(3)如图(2),过点B作BK⊥x轴交直线AC于点K,连接DK、AD,点H是DK的中点,点G是线段AK上任意一点,将△DGH沿GH边翻折得△DGH,求当KG为何值时,△DGH与△KGH重叠部分的面积是△DGK面积的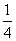 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com