Question

（本题满分8分）如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA＝∠CBD．

（1）求证：CD是⊙O的切线；
（2）若⊙O的半径为1，∠CBD＝30°，则图中阴影部分的面积；
（3）过点B作⊙O的切线交CD的延长线于点E若BC＝12，tan∠CDA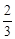＝，求BE的长．

Answer 1

（1）见解析    （2）－        （3）5

解析试题分析：（1）连接OD、OE，根据∠ADO+∠DBA=90°以及∠∠CDA=∠CBD得出∠ODC=90°；（2）阴影部分的面积等于△OCD的面积减去扇形ODA的面积进行计算；（3）将∠CDA转化成∠OEB，然后利用勾股定理进行求解.
试题解析：（1）证明：连OD，OE，∵AB为直径，∴∠ADB=90°，即∠ADO+∠BDO=90°，
又∵∠CDA=∠CBD，而∠CBD=∠BDO，∴∠BDO=∠CDA，∴∠CDA+∠ADO=90°，即∠CDO=90°，
∴CD是⊙O的切线；
、∵OD=1，∠CBD=30°    ∴∠DOC=60°  ∴∠C=30°   ∴OC=2，CD=
∴△OCD的面积=   扇形ODA的面积=   ∴阴影部分的面积=－；
（3）∵EB为⊙O的切线，∴ED=EB，OE⊥DB，∴∠ABD+∠DBE=90°，
∠OEB+∠DBE=90°，∴∠ABD=∠OEB，∴∠CDA=∠OEB．而tan∠CDA=，
∴tan∠OEB==，∵Rt△CDO∽Rt△CBE，∴，∴CD=×12=8，
在Rt△CBE中，设BE=x，∴（x+8）²=x²+12²，解得x=5．即BE的长为5．
考点：切线的判定、扇形的面积计算、锐角三角函数的求值