
【题目】如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.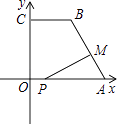
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
【答案】
(1)
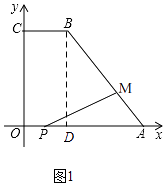
解:如图1,过点B作BD⊥x轴于点D,
∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10
(2)
解:∵AB=10,
∴10÷2=5,
∵0≤t≤5,
∴点M在AB上,
作ME⊥OA于E,
∴△AEM∽△ADB,
∴ ![]() ,
,
∴ ![]() ,
,
∴ME= ![]() t,
t,
∴S= ![]() PAME=
PAME= ![]() (10﹣t)
(10﹣t) ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() (t﹣5)2+20,
(t﹣5)2+20,
∵0≤t≤5,
∴t=5时,S取最大值,此时PA=10﹣t=5,
即:点P在OA的中点处
(3)
解:由题意可知:0≤t≤7,
当点P是直角顶点时,
∴PM⊥AP,
∴PA=10﹣t,
若0≤t≤5时,点M在AB上,如图2,
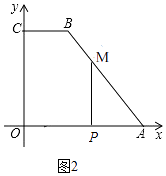
此时AM=2t,
∵cos∠BAO= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]()
∴t= ![]() ,
,
若5<t≤7时,点M在BC上,如图3,
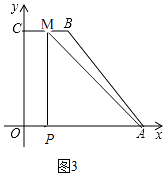
∴CM=14﹣2t,OP=t,
∴OP=CM,
∴t=14﹣2t,
∴t= ![]() ,
,
当点A是直角顶点时,
此时,∠MAP不可能为90°,此情况不符合题意;
当点M是直角顶点时,
若0≤t≤5时,M在AB上,如图4,
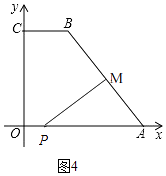
此时,AM=2t,AP=10﹣t
∵cos∠BAO= ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴t= ![]() ,
,
若5<t≤7时,点M在BC上,如图5,
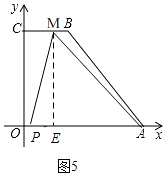
过点M作ME⊥x轴于点E,
此时,CM=14﹣2t,OP=t,
∴ME=8,PE=CM﹣OP=14﹣3t,
∴EA=10﹣(14﹣2t)=2t﹣4,
∵∠PMA=∠MEA=90°,
∴∠PME+∠EMA=∠EMA+∠MAP=90°,
∴∠PME=∠MAP,
∴△PME∽△MAE,
∴ ![]() ,
,
∴ME2=PEEA,
∴64=(14﹣3t)(2t﹣4),
∴3t2﹣8t+60=0,
△=﹣656<0,故此情况不存在;
综上所述,t= ![]() 或
或 ![]() ;
;
【解析】(1)过点B作BD⊥x轴于点D,利用勾股定理求出AB的长度;(2)先判断出点M在AB上,然后表示出PA,ME即可用三角形的面积公式即可;(3)△APM为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;利用锐角三角函数或相似三角形的性质即可.
【考点精析】认真审题,首先需要了解三角形的面积(三角形的面积=1/2×底×高),还要掌握三角形的稳定性(三角形的形状是固定的,三角形的这个性质叫做三角形的稳定性.三角形的这个性质在生产生活中应用很广,需要稳定的东西一般都制成三角形的形状)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.求所组成的两位数是5的倍数的概率.(请用“画树状图”或“列表”的方法写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,点E在边AD上,∠ABE=45°,BE=DE,连接BD,点P在线段DE上,过点P作PQ∥BD交BE于点Q,连接QD.设PD=x,△PQD的面积为y,则能表示y与x函数关系的图象大致是( )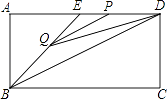
A.
B.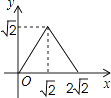
C.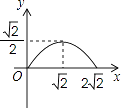
D.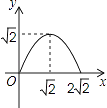
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°. 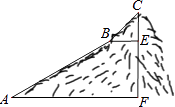
(1)求AB段山坡的高度EF;
(2)求山峰的高度CF.( ![]() 1.414,CF结果精确到米)
1.414,CF结果精确到米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准碟形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的剧烈为碟高.
(1)抛物线y=x2对应的碟宽为;抛物线y= ![]() x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
(2)利用图(1)中的结论:抛物线y=ax2﹣4ax﹣ ![]() (a>0)对应的碟宽为6,求抛物线的解析式.
(a>0)对应的碟宽为6,求抛物线的解析式.
(3)将抛物线yn=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3,…),定义F1 , F2 , …..Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为 ![]() ,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
①求抛物线y2的表达式;
②若F1的碟高为h1 , F2的碟高为h2 , …Fn的碟高为hn . 则hn= , Fn的碟宽右端点横坐标为 . 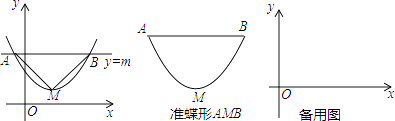
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )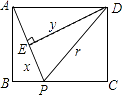
A.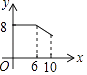
B.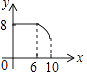
C.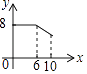
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.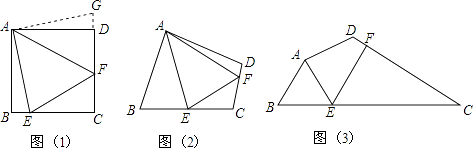
(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图1证明上述结论.
(2)【类比引申】
如图2,四边形ABCD中∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD
(3)【探究应用】如图3,在某公园的同一水平面上,四条通道围成的ABCD,已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ![]() ,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73).
=1.73).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com