
 (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A,
∠A, ∠A+2∠A=398°,
∠A+2∠A=398°, ∠A=134°
∠A=134° ∠A,
∠A, ∠A+360°-2∠A=398°,
∠A+360°-2∠A=398°, ∠A=142°
∠A=142° ∠A+2∠A=398°,从而求出∠A;
∠A+2∠A=398°,从而求出∠A; ∠A,由已知条件得,∠A+90°+
∠A,由已知条件得,∠A+90°+ ∠A+360°-2∠A=398°,从而求出∠A;然后针对这两种情况,分别求得∠BIC和∠BOC的大小.
∠A+360°-2∠A=398°,从而求出∠A;然后针对这两种情况,分别求得∠BIC和∠BOC的大小.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
 (2012•浦口区一模)提出问题:
(2012•浦口区一模)提出问题: ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:
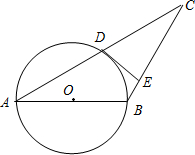 已知AB为⊙O的直径,点C为圆外一点,AC交⊙O 于点D,过点D作DE⊥BC于点E,AB=BC=4,∠ABC=120°.
已知AB为⊙O的直径,点C为圆外一点,AC交⊙O 于点D,过点D作DE⊥BC于点E,AB=BC=4,∠ABC=120°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
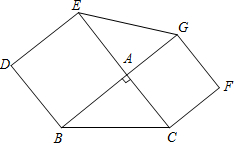 提出问题:
提出问题: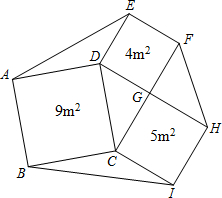 ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:
提出问题
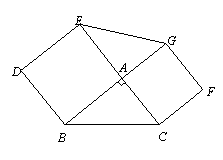
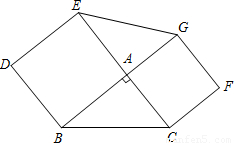
如图,在△ABC中,∠A=90°,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,小亮发现△ABC与△AEG面积相等.小亮思考:这个问题中,如果∠A≠90°,那么△ABC与△AEG面积是否仍然相等?
猜想结论
经过研究,小亮认为:上述问题中,对于任意△ABC,分别以边AB、AC向外作正方形ABDE 和正方形 ACFG,连接EG,那么△ABC与△AEG面积相等.
证明猜想
(1)请你帮助小亮画出图形,并完成证明过程.已知:以△ABC的两边AB、AC为边长分别向外作正方形ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
结论应用
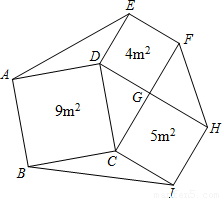
(2)学校教学楼前的一个六边形花圃被分成七个部分,分别种上不同品种的花卉,其中四边形ABCD、CIHG、GFED均为正方形,且面积分别为9m2、5m2和4m2.求这个六边形花圃ABIHFE的面积.
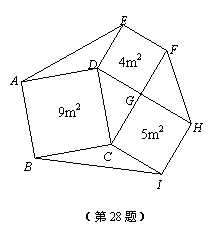 |
查看答案和解析>>
科目:初中数学 来源:2012年江苏省南京市联合体(秦淮下关浦口沿江)中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com