练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在正方形ABCD的外侧，作等边ADE，则BED的度数是 ．

    【答案】．

    【解析】

    试题分析：根据正方形的性质，可得AB与AD的关系，∠BAD的度数，根据等边三角形的性质，可得AE与AD的关系，∠AED的度数，根据等腰三角形的性质，可得∠AEB与∠ABE的关系，根据三角形的内角和，可得∠AEB的度数，根据角的和差，可得答案．∵四边形ABCD是正方形，∴AB=AD，∠BAD=90°．∵等边三角形ADE，∴AD=AE，∠DAE=∠AED=60°．∠BAE=∠BAD+∠DAE=90°+60°=150°，AB=AE，∠AEB=∠ABE=（180°﹣∠BAE）÷2=15°，∠BED=∠DAE﹣∠AEB=60°﹣15°=45°，故答案为：45°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，直线y＝kx＋b交x轴于点A，交y轴于点B，线段AB的中点E的坐标为(2，1)．

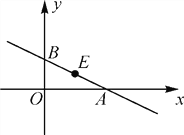
    (1)求k，b的值；

    (2)P为直线AB上一点，PC⊥x轴于点C，PD⊥y轴于点D，若四边形PCOD为正方形，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知购买1个足球和1个篮球共需130元，购买2个足球和3个篮球共需340元．

    （1）求每个足球和每个篮球的售价；

    （2）如果某校计划购买这两种球共54个，总费用不超过4000元，问最多可买多少个篮球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七年级各班分别选出3名学生组成班级代表队，参加知识竞赛，得分最多的班级为优胜班级，各代表队比赛结果如下：

    班级

    七（1）

    七（2）

    七（3）

    七（4）

    七（5）

    七（6）

    七（7）

    七（8）

    七（9）

    七（10）

    得分

    85

    90

    90

    100

    80

    100

    90

    80

    85

    90

    （1）写出表格中得分的众数、中位数；

    （2）学校从获胜班级的代表队中各抽取1名学生组成“绿色环保监督”小组，小明、小红分别是七（4）班和七（6）班代表队的学生，用列表法或画树状图的方法说明同时抽到小明和小红的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列3根小木棒能摆成三角形的是（　　）

    （1）5cm，12cm，13cm；（2）3cm，3cm，4cm；（3）4cm，3cm，7cm；（4）2cm，3cm，6cm．

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x2+（k﹣1）x+25是一个完全平方式，则常数k的值为________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，正六边形ABCDEF在直角坐标系内的位置如图所示，A（﹣2，0），点B在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2015次翻转之后，点B的坐标是________．

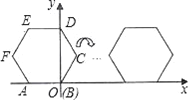
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做等邻边四边形．

    （1）如图1，四边形ABCD中，AC平分∠BAD，∠B=∠D．求证：四边形ABCD为等邻边四边形．

    （2）如图2，Rt△ABC中，∠ABC=90°，AB=2，BC=1，将△ABC沿∠ABC的平分线BB′的方向平移，得到△A′B′C′，连接AA′、BC′，若平移后的四边形ABC′A′是等邻边四边形，且满足BC′=AB，求平移的距离．

    （3）如图3，在等邻边四边形ABCD中，AB=AD，∠BAD+∠BCD=90°，AC和BD为四边形对角线，△BCD为等边三角形，试探究AC和AB的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】深圳今年4月份某星期的最高气温如下（单位℃）：26，25，27，28，27，25，25，则这个星期的最高气温的众数和中位数分别是（ ）
    A.25，26
    B.25，26.5
    C.27，26
    D.25，28

    查看答案和解析>>

    同步练习册答案