
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做等邻边四边形.
(1)如图1,四边形ABCD中,AC平分∠BAD,∠B=∠D.求证:四边形ABCD为等邻边四边形.
(2)如图2,Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC沿∠ABC的平分线BB′的方向平移,得到△A′B′C′,连接AA′、BC′,若平移后的四边形ABC′A′是等邻边四边形,且满足BC′=AB,求平移的距离.
(3)如图3,在等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC和BD为四边形对角线,△BCD为等边三角形,试探究AC和AB的数量关系.

【答案】(1)证明见解析;(2)平移的距离是![]() ;(3)AC=
;(3)AC=![]() AB,理由见解析.
AB,理由见解析.
【解析】(1)∵∠BAC=∠DAC ,∠B=∠D,AC=AC
∴△ABC≌△ADC
∴AB=AD
∴四边形ABCD是等邻边四边形.---------------------3’
(2)如图,延长C’B’交AB于点D ,
∵△A’B’C’由△ABC平移得到
∴A’B’∥AB,∠ A’B’C’=∠ABC=90°,C’B’=CB=1
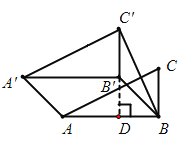
∴B’D⊥AB
∵BB’平分∠ABC,
∴∠B’BD=45°,即B’D=BD。
设B’D=BD=![]() ,∴C’D=1+
,∴C’D=1+![]() ,
,
∵BC’=AB=2,
∴Rt△BDC’中,![]() ,
,
解得![]() =
=![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
∴等腰Rt △BB’D中,BB’=![]() =
=![]()
(3)AC=![]() AB。
AB。
理由:如图,过A作AE⊥AB,且AE=AB,连接ED,EB
∵AE⊥AB
∴∠EAD+∠BAD=90°
又∵∠BAD+∠BCD=90°,△BCD为等边三角形
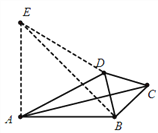
∴∠EAD=∠DCB=60°,
∵AE=AB,AB=AD ∴AE=AD
∴△AED为等边三角形,
∴AD=ED,∠EDA=∠BDC=60°
∴∠BDE=∠CDA,∵ED=AD,BD=CD
∴△BDE≌△CDA
∴AC=BE
∵AE=BE,∠BAE=90°, ∴BE=![]() AB,
AB,
∴AC=![]() AB
AB


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
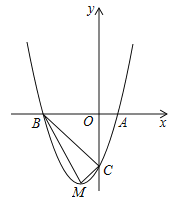
【题目】如图,顶点为M的抛物线y=a(x+1)2-4分别与x轴相交于点A,B(点A在点B的右侧),与y轴相交于点C(0,﹣3).
(1)求抛物线的函数表达式;
(2)判断△BCM是否为直角三角形,并说明理由.
(3)抛物线上是否存在点N(点N与点M不重合),使得以点A,B,C,N为顶点的四边形的面积与四边形ABMC的面积相等?若存在,求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人从学校到1000米远的展览馆去参观,甲走了5分钟后乙才出发,甲的速度是80米/分,乙的速度是180米/分,问乙多长时间能追上甲?追上甲时离展览馆还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象中,王刚同学观察得出了下面四条信息:(1)b2﹣4ac>0;(2)c>1;(3)2a﹣b<0;(4)a+b+c<0,其中错误的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于真命题的是( )
A. 同位角互补B. 多边形的外角和小于内角和
C. 平方根等于本身的数是1D. 同一平面内,垂直于同一条直线的两条直线平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com