
| A. | (b+c)(b-c)=a2 | B. | a=3+k,b=4+k,c=5+k(k>0) | ||
| C. | ∠A+∠B=∠C | D. | ∠A:∠B:∠C=1:3:2 |
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
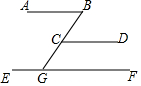 (1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$;
(1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
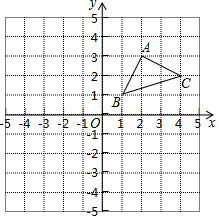 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1).
如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com