Question

19．如图1，已知A（a，1），B（2，b），且a，b满足（2a-3b-2）²+$\sqrt{a-2b}$=0．
（1）求A，B的坐标；
（2）在y轴上是否存在点P，使S_△PAB=1？若存在，直接写出满足条件的所有点P的坐标；若不存在，请说明理由．
（3）如图2，MB∥NO，点N在x轴上，OD平分∠AON，延长AB交OD于C，BC平分∠DBM，且∠D+$\frac{1}{2}$∠A=60°，求∠DBM的度数．

Answer 1

分析 （1）根据平方以及算术平方根的非负性进行计算；
（2）先作直线AB，根据构造三角形BPQ和三角形APQ，根据△APQ的面积-△BPQ的面积=1，求得点P的坐标；
（3）根据角平分线的定义和平行线的性质∠1=∠2=∠3=∠4+∠6，再根据外角的性质和角平分线的定义得出∠2=∠3=∠D+∠DBM，再根据三角形的内角和定理得出∠DBM．

解答 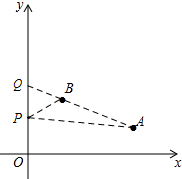解：（1）∵a，b满足（2a-3b-2）²+$\sqrt{a-2b}$=0，
∴$\left\{\begin{array}{l}{2a-3b-2=0}\\{a-2b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{a=4}\\{b=2}\end{array}\right.$，
∴A（4，1），B（2，2）；

（2）由A（4，1），B（2，2）可得
直线AB的解析式为：y=-$\frac{1}{2}$x+3，
当x=0时，y=3，
∴直线AB与y轴交于Q（0，3），
设点p的坐标为（0，y），则QP=|y-3|，
当S_△PAB=1时，△APQ的面积-△BPQ的面积=1，
即$\frac{1}{2}$×|y-3|×4-$\frac{1}{2}$×|y-3|×2=1，
解得y=4或2，
所以点P的坐标为（0，4），（0，2）；

（3）∵OD平分∠AON，
∴∠1=∠2，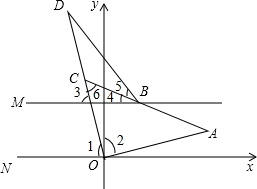
∵AN∥BM，
∴∠1=∠2=∠3=∠4+∠6，
又∵BC平分∠DBM，∠6=∠D+∠5，
∴∠4=∠5=$\frac{1}{2}$∠DBM，∠6=∠D+$\frac{1}{2}$∠DBM，
∴∠2=∠3=$\frac{1}{2}$∠DBM+（∠D+$\frac{1}{2}$∠DBM）=∠D+∠DBM，
在△AOC中，∠2+∠6+∠A=180°，
即（∠D+∠DBM）+（∠D+$\frac{1}{2}$∠DBM）+∠A=（2∠D+∠A）+$\frac{3}{2}$∠DBM=180°，
∵∠D+$\frac{1}{2}$∠A=60°，
∴2∠D+∠A=120°，
∴∠DBM=$\frac{2}{3}$（180°-120°）=40°．

点评 本题主要考查了坐标与图形性质，解决问题的关键是作辅助线构造三角形，根据三角形面积的和差关系进行计算，解题时注意分类思想的运用．