
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 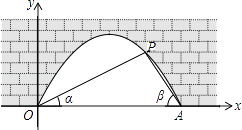
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
【答案】
(1)解:过点P作PH⊥OA于H,如图.
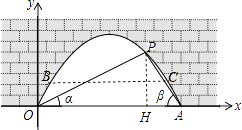
设PH=3x,
在Rt△OHP中,
∵tanα= ![]() =
= ![]() ,
,
∴OH=6x.
在Rt△AHP中,
∵tanβ= ![]() =
= ![]() ,
,
∴AH=2x,
∴OA=OH+AH=8x=4,
∴x= ![]() ,
,
∴OH=3,PH= ![]() ,
,
∴点P的坐标为(3, ![]() )
)
(2)解:若水面上升1m后到达BC位置,如图,

过点O(0,0),A(4,0)的抛物线的解析式可设为y=ax(x﹣4),
∵P(3, ![]() )在抛物线y=ax(x﹣4)上,
)在抛物线y=ax(x﹣4)上,
∴3a(3﹣4)= ![]() ,
,
解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x(x﹣4).
x(x﹣4).
当y=1时,﹣ ![]() x(x﹣4)=1,
x(x﹣4)=1,
解得x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ,
,
∴BC=(2+ ![]() )﹣(2﹣
)﹣(2﹣ ![]() )=2
)=2 ![]() =2×1.41=2.82≈2.8.
=2×1.41=2.82≈2.8.
答:水面上升1m,水面宽约为2.8米
【解析】(1)过点P作PH⊥OA于H,如图,设PH=3x,运用三角函数可得OH=6x,AH=2x,根据条件OA=4可求出x,即可得到点P的坐标;(2)若水面上升1m后到达BC位置,如图,运用待定系数法可求出抛物线的解析式,然后求出y=1时x的值,就可解决问题.


科目:初中数学 来源: 题型:
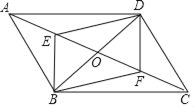
【题目】如图,ABCD的对角线AC、BD交于点O,E、F分别是AO、CO的中点,连接BE、DE、DF、BF,
(1)求证:四边形EBFD是平行四边形.
(2)求证:当AC=2BD时,四边形EBFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) 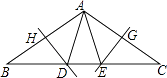
A.![]() =
= ![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.

(1)搭4条小鱼需要火柴棒_________根;
(2)搭n条小鱼需要火柴棒_____________根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图.
根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分?
(3)小明在书店停留了多少分钟?
(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 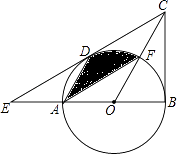
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
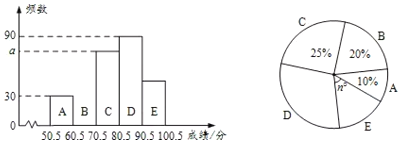
【题目】某校开展学生安全知识竞赛.现抽取部分学生的竞赛成绩(满分为100分,得分均为整数)进行统计,绘制了图中两幅不完整的统计图.根据图中信息,回答下列问题:
(1)a= ,n= ;
(2)补全频数分布直方图;
(3)该校共有2000名学生.若成绩在80分以上的为优秀,请你估计该校成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=b,移在动过程中,双曲线y=![]() (x>0)的图象始终经过BC的中点E,交AB于点D.
(x>0)的图象始终经过BC的中点E,交AB于点D.
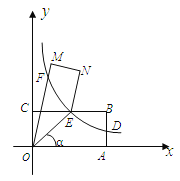
(1)证明:点D是AB的中点;
(2) 连结OE记∠AOE= α.
①当α=45°时,求 a、b之间的数量关系;
②当α=30°,k=![]() 时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
形OMNE除点E外的另一个交点为F,求直线DF的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )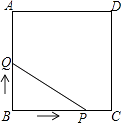
A.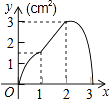
B.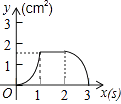
C.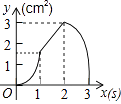
D.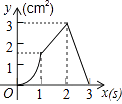
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com