
【题目】如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.

(1)搭4条小鱼需要火柴棒_________根;
(2)搭n条小鱼需要火柴棒_____________根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
【答案】(1)26;(2)6n+2;(3)m=14,有86条.
【解析】
(1)根据图形可得后一个图形中火柴数量是前一个图形火柴数量加6;
(2)根据题意找出规律即可得出结论;
(3)根据题意得6m+2=3m+44,可得答案.
(1)根据图形可得后一个图形中火柴数量是前一个图形火柴数量加6,根据题意,求出搭4条小鱼需要用6×4+2根火柴棒,即26根;
(2)第一个小鱼需要8根火柴棒,
第二个小鱼需要14根火柴棒,
第三个小鱼需要20根火柴棒;
∴每个小鱼比前一个小鱼多用6根火柴棒,
∴搭n条小鱼需要用8+6(n1)=(6n+2)根火柴棒.
故答案为:6n+2;
(3)由已知可得3m+44 = 2+6m,解得m=14,火柴总数=2+6×14=86.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.
(1)求函数y= ![]() x+2的图象上所有“中国结”的坐标;
x+2的图象上所有“中国结”的坐标;
(2)若函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读求绝对值不等式|x|<3和|x|>3的解集的过程:
因为|x|<3,从如图1所示的数轴上看:大于-3而小于3的数的绝对值是小于3的,所以|x|<3的解集是-3<x<3;
因为|x|>3,从如图2所示的数轴上看:小大于-3的数和大于3的数的绝对值是大于3的,所以|x|>3的解集是x<-3或x>3.
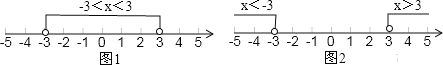
解答下面的问题:
(1)不等式|x|<a(a>0)的解集为______;不等式|x|>a(a>0)的解集为______.
(2)解不等式|x-5|<3;
(3)解不等式|x-3|>5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是__________
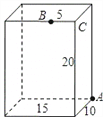
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
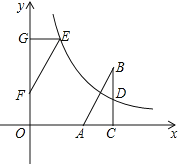
【题目】如图,在直角坐标系中,Rt△ABC的直角边AC在x轴上,∠ACB=90°,AC=1,反比例函数![]() (k>0)的图象经过BC边的中点D(3,1).
(k>0)的图象经过BC边的中点D(3,1).
(1)求这个反比例函数的表达式;
(2)若△ABC与△EFG成中心对称,且△EFG的边FG在y轴的正半轴上,点E在这个函数的图象上.
①求OF的长;
②连接AF,BE,证明四边形ABEF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 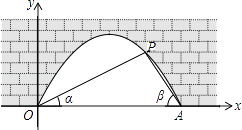
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
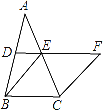
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB= ![]() ,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F. 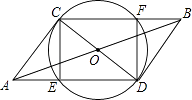
(1)问四边形CEDF是何种特殊四边形?请证明你的结论;
(2)当AC与⊙O相切时,四边形CEDF是正方形吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com