
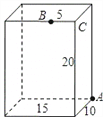
【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是__________
【答案】25
【解析】分析:求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.
详解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如图1:
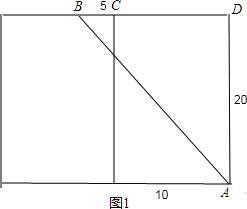
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=10+5=15cm,AD=20cm,
在直角三角形ABD中,根据勾股定理得:
∴AB=![]() =25cm;
=25cm;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图2:
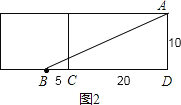
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5,
∴BD=CD+BC=20+5=25cm,AD=10cm,
在直角三角形ABD中,根据勾股定理得:
∴AB=![]() cm;
cm;
只要把长方体的右侧表面剪开与后面这个侧面所在的平面形成一个长方形,如图3:
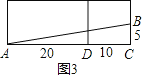
∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
∴AC=CD+AD=20+10=30cm,
在直角三角形ABC中,根据勾股定理得:
∴AB=![]() cm;
cm;
∵25<5![]() <5
<5![]() ,
,
∴自A至B在长方体表面的连线距离最短是25cm.
故答案为:25厘米


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】下面给出的五个结论中:
①最大的负整数是-1;②数轴上表示数3和-3的点到原点的距离相等;
③当a≤0时,|a|=-a成立;④若a2=9,则a一定等于3;
⑤![]() 一定是正数.说法正确的有_________________
一定是正数.说法正确的有_________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
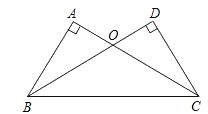
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.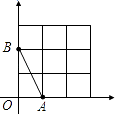
(1)求线段AB所在直线的函数解析式,并写出当0≤y≤2时,自变量x的取值范围;
(2)将线段AB绕点B逆时针旋转90°,得到线段BC,请在答题卡指定位置画出线段BC.若直线BC的函数解析式为y=kx+b,则y随x的增大而(填“增大”或“减小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) 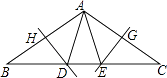
A.![]() =
= ![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点P(1,5)在函数![]() (x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )
(x>0)的图象上,过点P分别作x轴、y轴的垂线,垂足为点A,B;Q(m,n)为图象上另一动点,过点Q分别作x轴、y轴的垂线,垂足为点C、D.随着m的增大,四边形OCQD四边形OAPB不重叠部分的面积 ( )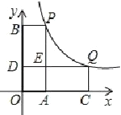
A. 先增大后减小 B. 先减小后增大
C. 先减小后增大再减小 D. 先增大后减小再增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.

(1)搭4条小鱼需要火柴棒_________根;
(2)搭n条小鱼需要火柴棒_____________根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 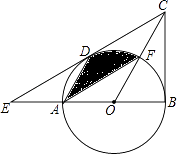
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)过多边形的一个顶点的所有对角线的条数与这些对角线分多边形所得的三角形个数的和为![]() ,求这个多边形的边数;
,求这个多边形的边数;
(2)过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为![]() 吗?若能,请求出这个多边形的边数;若不能,请说明理由.
吗?若能,请求出这个多边形的边数;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com