
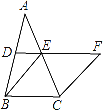
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
【答案】(1)证明见解析; (2)菱形的面积为8![]() .
.
【解析】试题分析:(1)从所给的条件可知,DE是△ABC中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=FE,所以是菱形;
(2)∠BCF是120°,所以∠EBC为60°,所以菱形的边长也为4,求出菱形的高面积就可求.
试题解析:(1)证明:∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC.又∵BE=2DE,EF=BE,∴EF=BC,EF∥BC,∴四边形BCFE是平行四边形.又∵BE=FE,∴四边形BCFE是菱形;
(2)解:∵∠BCF=120°,∴∠EBC=60°,∴△EBC是等边三角形,∴菱形的边长为4,高为2![]() ,∴菱形的面积为4×2
,∴菱形的面积为4×2![]() =8
=8![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
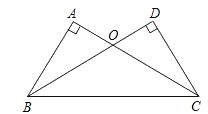
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.

(1)搭4条小鱼需要火柴棒_________根;
(2)搭n条小鱼需要火柴棒_____________根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. 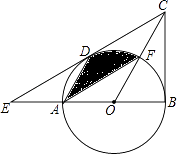
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
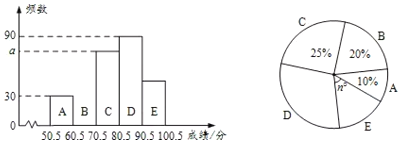
【题目】某校开展学生安全知识竞赛.现抽取部分学生的竞赛成绩(满分为100分,得分均为整数)进行统计,绘制了图中两幅不完整的统计图.根据图中信息,回答下列问题:
(1)a= ,n= ;
(2)补全频数分布直方图;
(3)该校共有2000名学生.若成绩在80分以上的为优秀,请你估计该校成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。
的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。

(1)求两个函数的解析式;
(2)观察图像,写出当x为何值时y1>y2?
(3)C、D分别是反比例函数![]() 第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标.
第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=b,移在动过程中,双曲线y=![]() (x>0)的图象始终经过BC的中点E,交AB于点D.
(x>0)的图象始终经过BC的中点E,交AB于点D.
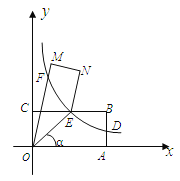
(1)证明:点D是AB的中点;
(2) 连结OE记∠AOE= α.
①当α=45°时,求 a、b之间的数量关系;
②当α=30°,k=![]() 时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
形OMNE除点E外的另一个交点为F,求直线DF的解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)过多边形的一个顶点的所有对角线的条数与这些对角线分多边形所得的三角形个数的和为![]() ,求这个多边形的边数;
,求这个多边形的边数;
(2)过多边形的一个顶点的所有对角线条数与这些对角线分多边形所得的三角形个数的和可能为![]() 吗?若能,请求出这个多边形的边数;若不能,请说明理由.
吗?若能,请求出这个多边形的边数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com