
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.
(1)求函数y= ![]() x+2的图象上所有“中国结”的坐标;
x+2的图象上所有“中国结”的坐标;
(2)若函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
【答案】
(1)
解:∵x是整数,x≠0时, ![]() x是一个无理数,
x是一个无理数,
∴x≠0时, ![]() x+2不是整数,
x+2不是整数,
∴x=0,y=2,
即函数y= ![]() x+2的图象上“中国结”的坐标是(0,2)
x+2的图象上“中国结”的坐标是(0,2)
(2)
解:①当k=1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:
(k≠0,k为常数)的图象上有且只有两个“中国结”:
(1,1)、(﹣1、﹣1);
②当k=﹣1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:
(k≠0,k为常数)的图象上有且只有两个“中国结”:
(1,﹣1)、(﹣1,1).
③当k≠±1时,函数y= ![]() (k≠0,k为常数)的图象上最少有4个“中国结”:
(k≠0,k为常数)的图象上最少有4个“中国结”:
(1,k)、(﹣1,﹣k)、(k,1)、(﹣k,﹣1),这与函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”矛盾,
(k≠0,k为常数)的图象上有且只有两个“中国结”矛盾,
综上可得,k=1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);
(k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);
k=﹣1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:(1,﹣1)、(﹣1、1).
(k≠0,k为常数)的图象上有且只有两个“中国结”:(1,﹣1)、(﹣1、1).
(3)
解:令(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k=0,
则[(k﹣1)x+k][(k﹣2)x+(k﹣1)]=0,
∴ 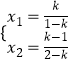
∴k= ![]() ,
,
整理,可得
x1x2+2x2+1=0,
∴x2(x1+2)=﹣1,
∵x1、x2都是整数,
∴ ![]() 或
或 ![]()
∴ ![]() 或
或 ![]()
①当 ![]() 时,
时,
∵ ![]() ,
,
∴k= ![]() ;
;
②当 ![]() 时,
时,
∵ ![]() ,
,
∴k=k﹣1,无解;
综上,可得
k= ![]() ,x1=﹣3,x2=1,
,x1=﹣3,x2=1,
y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k
=[ ![]() 2﹣3×
2﹣3× ![]() +2]x2+[2×(
+2]x2+[2×( ![]() )2﹣4×
)2﹣4× ![]() +1]x+(
+1]x+( ![]() )2﹣
)2﹣ ![]()
=﹣ ![]() x2﹣
x2﹣ ![]() x
x ![]()
①当x=﹣2时,
y=﹣ ![]() x2﹣
x2﹣ ![]() x
x ![]()
= ![]() ×(﹣2)2
×(﹣2)2 ![]() ×(﹣2)+
×(﹣2)+ ![]()
= ![]()
②当x=﹣1时,
y=﹣ ![]() x2﹣
x2﹣ ![]() x
x ![]()
= ![]() ×(﹣1)2
×(﹣1)2 ![]() ×(﹣1)+
×(﹣1)+ ![]()
=1
③当x=0时,y= ![]() ,
,
另外,该函数的图象与x轴所围成的平面图形中x轴上的“中国结”有3个:
(﹣2,0)、(﹣1、0)、(0,0).
综上,可得
若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,
该函数的图象与x轴所围成的平面图形中(含边界),一共包含有6个“中国结”:(﹣3,0)、(﹣2,0)、(﹣1,0)(﹣1,1)、(0,0)、(1,0)
【解析】(1)因为x是整数,x≠0时, ![]() x是一个无理数,所以x≠0时,
x是一个无理数,所以x≠0时, ![]() x+2不是整数,所以x=0,y=2,据此求出函数y=
x+2不是整数,所以x=0,y=2,据此求出函数y= ![]() x+2的图象上所有“中国结”的坐标即可.(2)首先判断出当k=1时,函数y=
x+2的图象上所有“中国结”的坐标即可.(2)首先判断出当k=1时,函数y= ![]() (k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);然后判断出当k≠1时,函数y=
(k≠0,k为常数)的图象上有且只有两个“中国结”:(1,1)、(﹣1、﹣1);然后判断出当k≠1时,函数y= ![]() (k≠0,k为常数)的图象上最少有4个“中国结”,据此求出常数k的值与相应“中国结”的坐标即可.(3)首先令(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k=0,则[(k﹣1)x+k][(k﹣2)x+(k﹣1)]=0,求出x1、x2的值是多少;然后根据x1、x2的值是整数,求出k的值是多少;最后根据横坐标,纵坐标均为整数的点称之为“中国结”,判断出该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”即可.
(k≠0,k为常数)的图象上最少有4个“中国结”,据此求出常数k的值与相应“中国结”的坐标即可.(3)首先令(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k=0,则[(k﹣1)x+k][(k﹣2)x+(k﹣1)]=0,求出x1、x2的值是多少;然后根据x1、x2的值是整数,求出k的值是多少;最后根据横坐标,纵坐标均为整数的点称之为“中国结”,判断出该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”即可.


科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.
(1)求∠CAE的度数;
(2)取AB边的中点F,连接CF、CE,试说明四边形AFCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出的五个结论中:
①最大的负整数是-1;②数轴上表示数3和-3的点到原点的距离相等;
③当a≤0时,|a|=-a成立;④若a2=9,则a一定等于3;
⑤![]() 一定是正数.说法正确的有_________________
一定是正数.说法正确的有_________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A. 一个数与它的倒数的积是1
B. 一个数的绝对值与它的相反数的商是![]()
C. 两个数的商为![]() ,这两个数互为相反数
,这两个数互为相反数
D. 两个数的积为1,这两个数互为倒数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用平方根去根号可以构造一个整系数方程.例如:x= ![]() +1时,移项得x﹣1=
+1时,移项得x﹣1= ![]() ,两边平方得(x﹣1)2=(
,两边平方得(x﹣1)2=( ![]() )2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x=
)2 , 所以x2﹣2x+1=2,即x2﹣2x﹣1=0.仿照上述构造方法,当x= ![]() 时,可以构造出一个整系数方程是( )
时,可以构造出一个整系数方程是( )
A.4x2+4x+5=0
B.4x2+4x﹣5=0
C.x2+x+1=0
D.x2+x﹣1=0
查看答案和解析>>
科目:初中数学 来源: 题型:
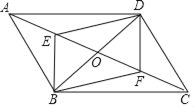
【题目】如图,ABCD的对角线AC、BD交于点O,E、F分别是AO、CO的中点,连接BE、DE、DF、BF,
(1)求证:四边形EBFD是平行四边形.
(2)求证:当AC=2BD时,四边形EBFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
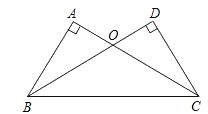
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用火柴棒按以下方式搭小鱼,是课本上多次出现的数学活动.

(1)搭4条小鱼需要火柴棒_________根;
(2)搭n条小鱼需要火柴棒_____________根;
(3)若搭n朵某种小花需要火柴棒(3n+44)根,现有一堆火柴棒,可以全部用上搭出m条小鱼,也可以全部用上搭出m朵小花,求m的值及这堆火柴棒的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com