练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】目前，步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗．对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同．若每消耗1千卡能量小明行走的步数比小红多10步，求小红每消耗1千卡能量需要行走多少步？

    【答案】小红每消耗1千卡能量需要行走30步．

    【解析】分析：设小红每消耗1千卡能量需要行走x步，则小明每消耗1千卡能量需要行走（x+10）步，根据数量关系消耗能量千卡数=行走步数÷每消耗1千卡能量需要行走步数结合小明步行12000步与小红步行9000步消耗的能量相同，即可得出关于x的分式方程，解之后经检验即可得出结论．

    详解：设小红每消耗1千卡能量需要行走x步，则小明每消耗1千卡能量需要行走（x+10）步，
    根据题意，得

    ，
    解得x=30．
    经检验：x=30是原方程的解．
    答：小红每消耗1千卡能量需要行走30步．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】现从A，B向甲、乙两地运送蔬菜，A，B两个蔬菜市场各有蔬菜14吨，其中甲地需要蔬菜15吨，乙地需要蔬菜13吨，从A到甲地运费50元/吨，到乙地30元/吨；从B地到甲运费60元/吨，到乙地45元/吨．

    （1）设A地到甲地运送蔬菜x吨，请完成下表：

    运往甲地（单位：吨）

    运往乙地（单位：吨）

    A

    x

    B

    （2）设总运费为W元，请写出W与x的函数关系式

    （3）怎样调运蔬菜才能使运费最少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，D、E在AB上，且D、E分别是AC、BC的垂直平分线上一点；若△CDE的周长为4，则AB的长为___________；若∠ACB=100°，则∠DCE=_________度；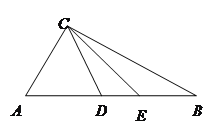

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，D、E是BC边上的点，连接AD，AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD=CD′；

    （1）求证：△ABD≌△ACD′；

    （2）若∠BAC=120°，求∠DAE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题8分）△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．

    （1）按要求作图：

    ①画出△ABC关于原点O的中心对称图形△A1B1C1；

    ②画出将△ABC绕点A逆时针旋转90°得到△AB2C2，

    （2）回答下列问题：

    ①△A1B1C1中顶点A1坐标为 ；②若P（a，b）为△ABC边上一点，则按照（1）中①作图，点P对应的点P1的坐标为 ．

    【答案】（1）作图见解析；（2）（1，-2）（-a,-b）

    【解析】试题分析：（1）首先找出对应点的位置，再顺次连接即可；

    （2）①根据图形可直接写出坐标；②根据关于原点对称点的坐标特点可得答案．

    试题解析：（1）如图所示：

    （2）①根据图形可得A1坐标为（2，﹣4）；

    ②点P1的坐标为（﹣a，﹣b）．

    故答案为：（﹣2，﹣4）；（﹣a，﹣b）．

    考点：作图-旋转变换．

    【题型】填空题
    【结束】
    23

    【题目】在学习了“普查与抽样调查”之后，某校八（1）班数学兴趣小组对该校学生的视力情况进行了抽样调查，并画出了如图所示的条形统计图．请根据图中信息解决下列问题：

    （1）本次抽查活动中共抽查了　　名学生；

    （2）已知该校七年级、八年级、九年级学生数分别为360人、400人、540人．

    ①试估算：该校九年级视力不低于4.8的学生约有　　名；

    ②请你帮忙估算出该校视力低于4.8的学生数．

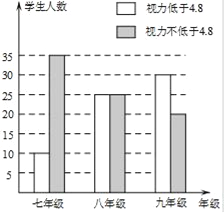
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，1925年数学家莫伦发现的世界上第一个完美长方形，它恰能被分割成10个大小不同的正方形.若标注①、②的正方形边长分别为5和6，请你直接写出以下数据：

    （1）第6个正方形的边长= ；

    （2）第8个正方形的边长= ；

    （3）整个长方形的面积= .

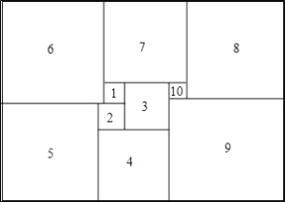
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图．

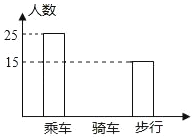
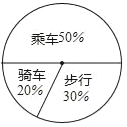
    （1）求该班有多少名学生？

    （2）补上骑车分布直方图的空缺部分；

    （3）在扇形统计图中，求步行人数所占的圆心角度数；

    （4）若全年级有900人，估计该年级骑车人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，我们不妨将横坐标，纵坐标均为整数的点称之为“中国结”．
    （1）求函数y= x+2的图象上所有“中国结”的坐标；
    （2）若函数y= （k≠0，k为常数）的图象上有且只有两个“中国结”，试求出常数k的值与相应“中国结”的坐标；
    （3）若二次函数y=（k2﹣3k+2）x2+（2k2﹣4k+1）x+k2﹣k（k为常数）的图象与x轴相交得到两个不同的“中国结”，试问该函数的图象与x轴所围成的平面图形中（含边界），一共包含有多少个“中国结”？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请阅读求绝对值不等式|x|＜3和|x|＞3的解集的过程：

    因为|x|＜3，从如图1所示的数轴上看：大于-3而小于3的数的绝对值是小于3的，所以|x|＜3的解集是-3＜x＜3；

    因为|x|＞3，从如图2所示的数轴上看：小大于-3的数和大于3的数的绝对值是大于3的，所以|x|＞3的解集是x＜-3或x＞3．

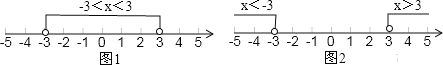
    解答下面的问题：

    （1）不等式|x|＜a（a＞0）的解集为______；不等式|x|＞a（a＞0）的解集为______．

    （2）解不等式|x-5|＜3；

    （3）解不等式|x-3|＞5．

    查看答案和解析>>

    同步练习册答案