
【题目】如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.

 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.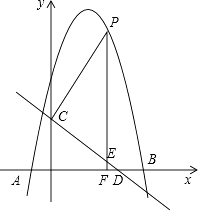
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.
(1)求∠CAE的度数;
(2)取AB边的中点F,连接CF、CE,试说明四边形AFCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)写出方程 x + y =3的两个解__________,把方程 x + y =3化成一次函数的形式为__________;
(2)以方程 x + y =3的解为坐标的所有点组成的图象与一次函数 y =3- x 的图象相同吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小明步行12 000步与小红步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步数比小红多10步,求小红每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出的五个结论中:
①最大的负整数是-1;②数轴上表示数3和-3的点到原点的距离相等;
③当a≤0时,|a|=-a成立;④若a2=9,则a一定等于3;
⑤![]() 一定是正数.说法正确的有_________________
一定是正数.说法正确的有_________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O.
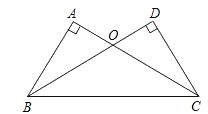
(1)求证:△ABO≌△DCO;
(2)△OBC是何种三角形?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com