
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.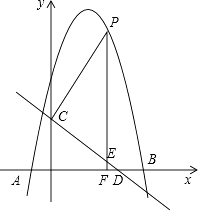
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:将点A、B坐标代入抛物线解析式,得:
![]() ,解得
,解得 ![]() ,
,
∴抛物线的解析式为:y=﹣x2+4x+5
(2)
解:∵点P的横坐标为m,
∴P(m,﹣m2+4m+5),E(m,﹣ ![]() m+3),F(m,0).
m+3),F(m,0).
∴PE=|yP﹣yE|=|(﹣m2+4m+5)﹣(﹣ ![]() m+3)|=|﹣m2+
m+3)|=|﹣m2+ ![]() m+2|,
m+2|,
EF=|yE﹣yF|=|(﹣ ![]() m+3)﹣0|=|﹣
m+3)﹣0|=|﹣ ![]() m+3|.
m+3|.
由题意,PE=5EF,即:|﹣m2+ ![]() m+2|=5|﹣
m+2|=5|﹣ ![]() m+3|=|
m+3|=| ![]() m+15|
m+15|
①若﹣m2+ ![]() m+2=
m+2= ![]() m+15,整理得:2m2﹣17m+26=0,
m+15,整理得:2m2﹣17m+26=0,
解得:m=2或m= ![]() ;
;
②若﹣m2+ ![]() m+2=﹣(
m+2=﹣( ![]() m+15),整理得:m2﹣m﹣17=0,
m+15),整理得:m2﹣m﹣17=0,
解得:m= ![]() 或m=
或m= ![]() .
.
由题意,m的取值范围为:﹣1<m<5,故m= ![]() 、m=
、m= ![]() 这两个解均舍去.
这两个解均舍去.
∴m=2或m= ![]()
(3)
解:假设存在.
作出示意图如下:
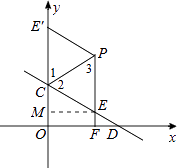
∵点E、E′关于直线PC对称,
∴∠1=∠2,CE=CE′,PE=PE′.
∵PE平行于y轴,∴∠1=∠3,
∴∠2=∠3,∴PE=CE,
∴PE=CE=PE′=CE′,即四边形PECE′是菱形.
当四边形PECE′是菱形存在时,
由直线CD解析式y=﹣ ![]() x+3,可得OD=4,OC=3,由勾股定理得CD=5.
x+3,可得OD=4,OC=3,由勾股定理得CD=5.
过点E作EM∥x轴,交y轴于点M,易得△CEM∽△CDO,
∴ ![]() ,即
,即 ![]() ,解得CE=
,解得CE= ![]() |m|,
|m|,
∴PE=CE= ![]() |m|,又由(2)可知:PE=|﹣m2+
|m|,又由(2)可知:PE=|﹣m2+ ![]() m+2|
m+2|
∴|﹣m2+ ![]() m+2|=
m+2|= ![]() |m|.
|m|.
①若﹣m2+ ![]() m+2=
m+2= ![]() m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣
m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣ ![]() ;
;
②若﹣m2+ ![]() m+2=﹣
m+2=﹣ ![]() m,整理得:m2﹣6m﹣2=0,解得m1=3+
m,整理得:m2﹣6m﹣2=0,解得m1=3+ ![]() ,m2=3﹣
,m2=3﹣ ![]() .
.
由题意,m的取值范围为:﹣1<m<5,故m=3+ ![]() 这个解舍去.
这个解舍去.
当四边形PECE′是菱形这一条件不存在时,
此时P点横坐标为0,E,C,E'三点重合与y轴上,也符合题意,
∴P(0,5)
综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)
方法二:
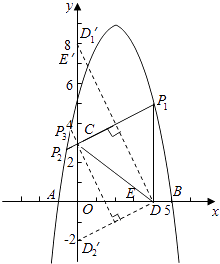
若E(不与C重合时)关于直线PC的对称点E′在y轴上,则直线CD与直线CE′关于PC轴对称.
∴点D关于直线PC的对称点D′也在y轴上,
∴DD′⊥CP,∵y=﹣ ![]() x+3,
x+3,
∴D(4,0),CD=5,
∵OC=3,
∴OD′=8或OD′=2,
①当OD′=8时,D′(0,8),设P(t,﹣t2+4t+5),D(4,0),C(0,3),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() ,
,
∴2t2﹣7t﹣4=0,
∴t1=4,t2=﹣ ![]() ,
,
②当OD′=2时,D′(0,﹣2),
设P(t,﹣t2+4t+5),
∵PC⊥DD′,∴KPC×KDD′=﹣1,
∴ ![]() =﹣1,
=﹣1,
∴t1=3+ ![]() ,t2=3﹣
,t2=3﹣ ![]() ,
,
∵点P是x轴上方的抛物线上一动点,
∴﹣1<t<5,
∴点P的坐标为(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3).
﹣3).
若点E与C重合时,P(0,5)也符合题意.
综上所述,存在满足条件的点P,可求得点P坐标为(0,5),(﹣ ![]() ,
, ![]() ),(4,5),(3﹣
),(4,5),(3﹣ ![]() ,2
,2 ![]() ﹣3)
﹣3)
【解析】(1)利用待定系数法求出抛物线的解析式;(2)用含m的代数式分别表示出PE、EF,然后列方程求解;(3)解题关键是识别出当四边形PECE′是菱形,然后根据PE=CE的条件,列出方程求解;当四边形PECE′是菱形不存在时,P点y轴上,即可得到点P坐标.


科目:初中数学 来源: 题型:
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度. (结果保留整数,参考数据:sin35°≈ ![]() ,cos35°≈
,cos35°≈ ![]() ,tan35°≈
,tan35°≈ ![]() ,
, ![]() ≈1.7)
≈1.7)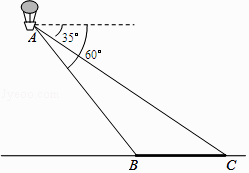
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB∥DE,AF∥DC,E、F两点在BC上,且四边形AEFD是平行四边形.
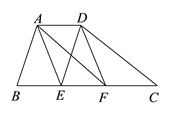
(1)AD与BC有何等量关系?请说明理由;
(2)当AB=DC时,求证:四边形AEFD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( )
①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离;

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
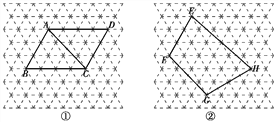
【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A | x | |
B |
(2)设总运费为W元,请写出W与x的函数关系式
(3)怎样调运蔬菜才能使运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由
如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.将∠E=∠1的过程填写完整.
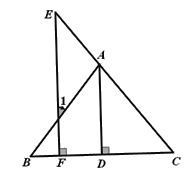
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意义 )
∴AD//EF
∴∠1= ()
∠E= ()
又∵AD平分∠BAC(已知 )
∴ =
∴∠1=∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是BC边上的点,连接AD,AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′;
(1)求证:△ABD≌△ACD′;
(2)若∠BAC=120°,求∠DAE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com