
【题目】填写推理理由
如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.将∠E=∠1的过程填写完整.
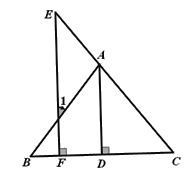
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意义 )
∴AD//EF
∴∠1= ()
∠E= ()
又∵AD平分∠BAC(已知 )
∴ =
∴∠1=∠E.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义一种新运算⊙:1⊙3=1×4+3=7; 3⊙(-1)=3×4-1=11;(-5)⊙4=(-5)×4+4=-16; (-4)⊙(-3)=(-4)×4-3=-19.
(1)由以上式子可知:a⊙b= ;
(2)若a⊙(-2b)=4,请计算(a-b)⊙(2a+b)的值;
(3)若[x⊙(-2)] ⊙ [(-x)⊙2]=6,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(5,0)两点,直线y=﹣ ![]() x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.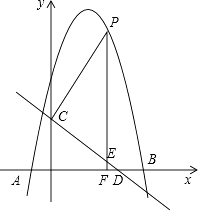
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校测量了九年级(1)班学生的身高(精确到1cm),按10cm为一段进行分组,得到如下频数分布直方图如图,则下列说法不正确的是( )

A. 该班人数最多的身高段的学生数为20人
B. 该班身高低于160.5 cm的学生数为20人
C. 该班身高最高段的学生数为20人
D. 该班身高最高段的学生数为7人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x | 人数 |
60≤x<80 | 2 |
80≤x<100 | 5 |
100≤x<120 | 21 |
120≤x<140 | 13 |
140≤x<160 | 8 |
160≤x<180 | 4 |
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是BC边的中点,以AD为边作等边△ADE.
(1)求∠CAE的度数;
(2)取AB边的中点F,连接CF、CE,试说明四边形AFCE是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出的五个结论中:
①最大的负整数是-1;②数轴上表示数3和-3的点到原点的距离相等;
③当a≤0时,|a|=-a成立;④若a2=9,则a一定等于3;
⑤![]() 一定是正数.说法正确的有_________________
一定是正数.说法正确的有_________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com