
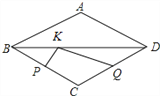
【题目】如图,点P、Q是边长为2的菱形ABCD中两边BC和CD的中点,K是BD上一动点,则KP+KQ的最小值为________.
 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
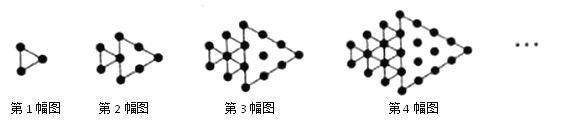
【题目】如图所示,将形状、大小完全相同的“![]() ”和线段按照一定规律摆成下列图形.第1幅图形中“
”和线段按照一定规律摆成下列图形.第1幅图形中“![]() ”的个数为
”的个数为![]() ,第2幅图形中“
,第2幅图形中“![]() ”的个数为
”的个数为![]() ,第3幅图形中“
,第3幅图形中“![]() ”的个数为
”的个数为![]() ,……,以此类推,解决以下问题:
,……,以此类推,解决以下问题:
(1)直接写出![]() ,
,![]() (用含n的代数式表示);
(用含n的代数式表示);
(2)猜想是否存在某幅图中“![]() ”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
(3)求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
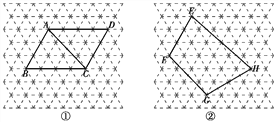
【题目】图中的虚线网格是等边三角形网格,它的每一个小三角形都是边长为1的等边三角形.
(1)边长为1的等边三角形的高=____;
(2)图①中的ABCD的对角线AC的长=____;
(3)图②中的四边形EFGH的面积=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,某市政府的一项实事工程就是由政府投入1 000万元资金,对城区4万户家庭的老式水龙头和13升抽水马桶进行免费改造,某社区为配合政府完成该项工作,对社区内1 200户家庭中的120户进行了随机抽样调查,并汇总成下表:
改造情况 | 均不改造 | ||||||
改造水龙头 | 改造马桶 | ||||||
1个 | 2个 | 3个 | 4个 | 1个 | 2个 | ||
户数 | 20 | 31 | 28 | 21 | 12 | 69 | 2 |
(1)试估计该社区需要对水龙头或马桶进行改造的家庭共有___户;
(2)改造后,一个水龙头一年大概可节约5吨水,一个马桶一年大约可节约15吨水,试估计该社区一年共可节约多少吨水?
(3)在抽样的120户家庭中,既要改造水龙头又要改造马桶的家庭共有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由
如图,已知AD⊥BC于D,EF⊥BC于F,AD平分∠BAC.将∠E=∠1的过程填写完整.
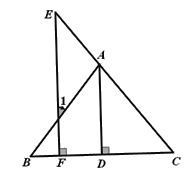
解:解:∵AD⊥BC, EF⊥BC( 已知 )
∴∠ADC=∠EFC= 90°( 垂直的意义 )
∴AD//EF
∴∠1= ()
∠E= ()
又∵AD平分∠BAC(已知 )
∴ =
∴∠1=∠E.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如图两幅统计图(不完整).
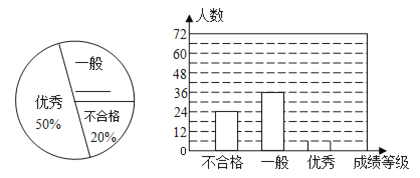
请你根据图中所给的信息解答下列问题:
(1)这次测试,一共抽取了名学生;
(2)请将以上两幅统计图补充完整;(注:扇形图补百分比,条形图补“优秀”人数与高度);
(3)若“一般”和“优秀”均被视为达标成绩,该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,B在x轴上,四边形OACB为平行四边形,且∠AOB=60°,反比例函数![]() (k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(k>0)在第一象限内过点A,且与BC交于点F.(1)若OA=10,求反比例函数的解析式;
(2)若F为BC的中点,且S△AOF=24![]() ,求OA长及点C坐标;
,求OA长及点C坐标;
(3)在(2)的条件下,过点F作EF∥OB交OA于点E(如图2),若点P是直线EF上一个动点,连结,PA,PO,问是否存在点P,使得以P,A,O三点构成的三角形是直角三角形?若存在,请指出这样的P点有几个,并直接写出其中二个P点坐标;若不存在,请说明了理由.
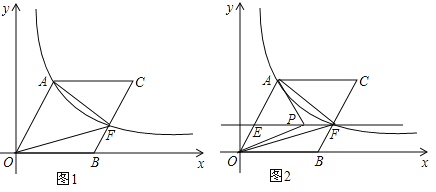
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为疏导国庆假期交通,一辆交通巡逻车在南北公路上巡视.某天早上从![]() 地出发,中午到达
地出发,中午到达![]() 地,行驶记录如下(规定向北为正方向,单位:千米):
地,行驶记录如下(规定向北为正方向,单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
请你解答下列问题:
(1)![]() 地在
地在![]() 地的什么方向?与
地的什么方向?与![]() 地相距多远?
地相距多远?
(2)巡逻车在巡逻中,离开![]() 地最远多少千米?
地最远多少千米?
(3)若巡逻车行驶每千米耗油![]() 升,这半天共耗油多少升?
升,这半天共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com