【题目】定义一种新运算⊙：1⊙3＝1×4＋3＝7； 3⊙(－1)＝3×4－1＝11；(－5)⊙4＝(－5)×4＋4＝－16； (－4)⊙(－3)＝(－4)×4－3＝－19.
(1)由以上式子可知：a⊙b＝ ；
(2)若a⊙(－2b)＝4，请计算(a－b)⊙(2a＋b)的值；
(3)若[x⊙(－2)] ⊙ [(－x)⊙2]＝6，求x的值.
【答案】⑴a⊙b＝4a+b；⑵ 6；⑶
【解析】
试题（1）根据题目中的式子可以猜出a⊙b的结果；
（2）根据（1）中的结果分别计算：a⊙(－2b)＝4和(a－b)⊙(2a＋b)即可求值；
（3）根据（1）中的结果进行解方程即可.
试题解析：（1）由题目中的式子可得，
a⊙b=4a+b，
（2）由（1）得：a⊙(－2b)=4a-2b=4，即：2a-b=2.
∴(a－b)⊙(2a＋b)=4（a-b）+2a+b=6a-3b=3(2a-b)=3×2=6；
（3）[x⊙(－2)] ⊙ [(－x)⊙2]=(4x-2) ⊙(-4x+2)=4(4x-2)-4x+2=12x-6
∴12x-6=6
解得：x=1.
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案科目：初中数学 来源： 题型：
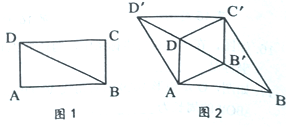
【题目】如图l，BD是矩形ABCD的对角线，∠ABD=30
，AD=1．将△BCD沿射线BD方向平移到△B'C'D'的位置，使B'为BD中点，连接AB’，C'D，AD’，BC’，如图2．
(1)求证：四边形AB'C'D是菱形：
(2)四边形ABC'D'的周长为____：
(3)将四边形ABC'D’沿它的两条对角线剪开，用得到的四个三角形拼成与其面积相等的矩形，直接写出可能拼成的矩形的周长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小明在热气球A上看到正前方横跨河流两岸的大桥BC，并测得B，C两点的俯角分别为60°和35°，已知大桥BC的长度为100m，且与地面在同一水平面上．求热气球离地面的高度． （结果保留整数，参考数据：sin35°≈ 
，cos35°≈ 
，tan35°≈ 
， 
≈1.7）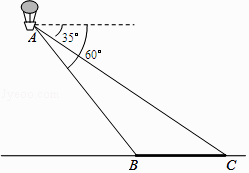
查看答案和解析>>
科目：初中数学 来源： 题型：
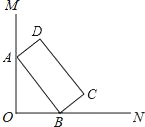
【题目】如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为（ ）
A. 
+1 B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
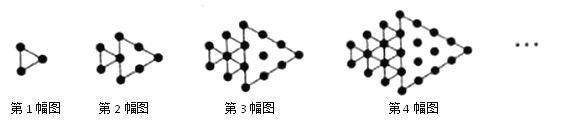
【题目】如图所示，将形状、大小完全相同的“
”和线段按照一定规律摆成下列图形.第1幅图形中“”的个数为
，第2幅图形中“”的个数为
，第3幅图形中“”的个数为
，……，以此类推，解决以下问题：
（1）直接写出
，
（用含n的代数式表示）；
（2）猜想是否存在某幅图中“”的个数为2018，若存在，直接写出n的值；若不存在，则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数，并直接写出此时n的值；
（3）求出
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB表示路灯，当身高为1.6米的小名站在离路灯1.6的D处时，他测得自己在路灯下的影长DE与身高CD相等，当小明继续沿直线BD往前走到E点时，画出此时小明的影子，并计算此时小明的影长． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在BC上，且四边形AEFD是平行四边形．
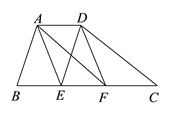
（1）AD与BC有何等量关系？请说明理由；
（2）当AB=DC时，求证：四边形AEFD是矩形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】填写推理理由
如图，已知AD⊥BC于D，EF⊥BC于F，AD平分∠BAC.将∠E＝∠1的过程填写完整．
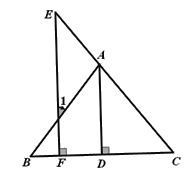
解：解：∵AD⊥BC, EF⊥BC（ 已知 ）
∴∠ADC=∠EFC= 90°（ 垂直的意义 ）
∴AD//EF
∴∠1= （）
∠E= （）
又∵AD平分∠BAC（已知 ）
∴ =
∴∠1=∠E.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com