
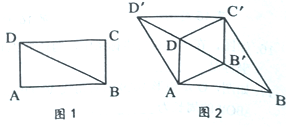
����Ŀ����ͼl��BD�Ǿ���ABCD�ĶԽ��ߣ���ABD=30![]() ��AD=1������BCD������BD����ƽ�Ƶ���B'C'D'��λ�ã�ʹB'ΪBD�е㣬����AB����C'D��AD����BC������ͼ2��
��AD=1������BCD������BD����ƽ�Ƶ���B'C'D'��λ�ã�ʹB'ΪBD�е㣬����AB����C'D��AD����BC������ͼ2��
(1)��֤���ı���AB'C'D�����Σ�
(2)�ı���ABC'D'���ܳ�Ϊ____��
(3)���ı���ABC'D�������������Խ��������õõ����ĸ�������ƴ�����������ȵľ��Σ�ֱ��д������ƴ�ɵľ��ε��ܳ�.
���𰸡���1��֤������������2��4![]() ����2��3+2
����2��3+2![]() ��6+
��6+![]()
�������������������1����һ���ڱ���ȵ�ƽ���ı��������Σ��ݴ˽���֤�����ɣ�
��2�����ж��ı���ABC'D'�����Σ��ٸ��ݱ߳�AB=![]() AD=
AD=![]() �����ɵõ��ı���ABC'D�����ܳ�Ϊ4
�����ɵõ��ı���ABC'D�����ܳ�Ϊ4![]() ��
��
��3���������ֲ�ͬ��ƴ�����ֱ���ÿ���ƴ�ɵľ����ܳ�
�����������1����BD�Ǿ���ABCD�ĶԽ��ߣ���ABD=30����
���ADB=60����
��ƽ�ƿɵã�B'C'=BC=AD����D'B'C'=��DBC=��ADB=60����
��AD��B'C'
���ı���AB'C'D��ƽ���ı��Σ�
��B'ΪBD�е㣬
��Rt��ABD��AB'=![]() BD=DB'��
BD=DB'��
���ߡ�ADB=60����
���ADB'�ǵȱ������Σ�
��AD=AB'��
���ı���AB'C'D�����Σ�
��2����ƽ�ƿɵã�AB=C'D'����ABD'=��C'D'B=30����
��AB��C'D'��
���ı���ABC'D'��ƽ���ı��Σ�
�ɣ�1���ɵã�AC'��B'D��
���ı���ABC'D'�����Σ�
��AB=![]() AD=
AD=![]() ��
��
���ı���ABC'D�����ܳ�Ϊ4![]() ��
��
��3�����ı���ABC'D'�����������Խ��������õõ����ĸ�������ƴ�����������ȵľ������£�
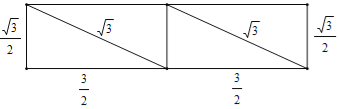
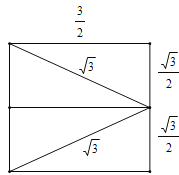
�������ܳ�Ϊ6+![]() ��2
��2![]() +3��
+3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C=90�㣬M��AB���е㣬����P�ӵ�A��������AC���������˶����յ�C������Q�ӵ�C��������CB���������˶����յ�B����֪P��Q����ͬʱ��������ͬʱ�����յ㣬����MP��MQ��PQ���������˶������У���MPQ�������С�仯����ǣ� ��
A.һֱ����
B.һֱ��С
C.�ȼ�С������
D.����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ĸ���������AB=BC���ڡ�ABC=90![]() ����AC=BD����AC��BD������ѡȡ������Ϊ����������ʹ��BCDΪ�����Σ���ͼ����������������ѡ�������д������ ( )
����AC=BD����AC��BD������ѡȡ������Ϊ����������ʹ��BCDΪ�����Σ���ͼ����������������ѡ�������д������ ( )
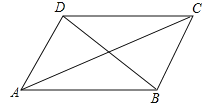
A. �ڢ� B. �ڢ� C. �٢� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��1��3��x2��2x��1����4(3x��2)+2(x��1)������x=��3��
��2��2a2��[![]() ��ab��4a2��+8ab]��
��ab��4a2��+8ab]��![]() ab������a=1��b=
ab������a=1��b=![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ְ������������ij��˾��Ʊ1000����ÿ��28Ԫ���������������첻���ף��±�Ϊ������ÿ�ոù�Ʊ���ǵ����������λ��Ԫ��

��1��ͨ���ϱ�����Ϊ����������ʱ��ÿ���Ƕ���Ԫ��
��2��������ÿ������Ƕ��٣�����Ƕ���Ԫ��
��3����֪��Ʊ����ʱ�轻�ɽ���1.5���Ľ���������ʱ�轻�ɽ���2.5���Ľ��ѣ����������׳�����С��ְ���ʹ�Ʊ����ӯ����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
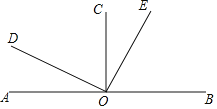
����Ŀ����ͼ����ֱ֪��AB��һ��O��OC��AB��OD��OE, ����COE=![]() ��BOD.
��BOD.
��1�����COE, ��BOD, ��AOE�Ķ���.
��2����OFƽ�֡�BOE�����AOF�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=10��BC=8��PΪAD���е㣬����ABP��BP��������EBP����A�䵽��E����������DE����ͼ�����APB��ȵĽǵĸ���Ϊ�� �� 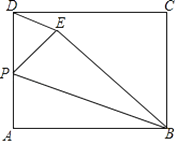
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��A1B1C1D1���ⳤΪ1���ڡ��������dz�ͬʱ�ӵ�A����������ͬ���ٶȷֱ�������ǰ���У��ڼdz����е�·����AA1��A1D1�������dz����е�·����AB��BB1���������Ҷ���ѭ���¹��������еĵ�n��2���n�������ڵ�ֱ�߱����ǼȲ�ƽ��Ҳ���ཻ������n��������������ô���ڡ��������dz���������2013����ֱ�ֹͣ�������������嶥�㴦ʱ������֮��ľ����� ��
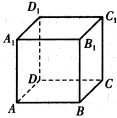
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��������ѣ�1��3��1��4��3��7�� 3��(��1)��3��4��1��11��(��5)��4��(��5)��4��4����16�� (��4)��(��3)��(��4)��4��3����19.
(1)������ʽ�ӿ�֪��a��b�� ��
(2)��a��(��2b)��4�������(a��b)��(2a��b)��ֵ��
(3)��[x��(��2)] �� [(��x)��2]��6����x��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com