
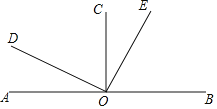
【题目】如图,已知直线AB上一点O,OC⊥AB,OD⊥OE, 若∠COE=![]() ∠BOD.
∠BOD.
(1)求∠COE, ∠BOD, ∠AOE的度数.
(2)若OF平分∠BOE,求∠AOF的度数.
【答案】(1)120°;(2)150°
【解析】
试题(1)由于∠COE=![]() ∠BOD,可设∠COE=x,则∠BOD=5x,列出方程即可求出x的值,进而求出∠COE,∠BOD,∠AOE的度数.
∠BOD,可设∠COE=x,则∠BOD=5x,列出方程即可求出x的值,进而求出∠COE,∠BOD,∠AOE的度数.
(2)作出∠BOE的角平分线后求出∠BOF的度数即可求出∠AOF的度数.
解: (1)∵∠COE=![]() ∠BOD
∠BOD
∴设∠COE=x,则∠BOD=5x
∵OD⊥OE, ∴∠DOE=90°,
∴∠BOE=∠BOD-∠DOE=5x-90°
∵OC⊥AB, ∴∠BOC=90°, ∴∠COE+∠BOE=90°
∴x+5x-90=90, x=30°
∴∠COE=30°
∴∠BOD=5x=150°
∴∠AOE=∠AOC+∠COE=90+30=120°
(2)作OF平分∠BOE
∴∠BOF=![]() ∠BOE
∠BOE
∵∠BOE=90°-∠COE=60°, ∴∠BOF=30°
∴∠AOF=180°-∠BOF=150°


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,将△ABC纸片沿中位线EH折叠,使点A对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.




(1)将□ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段_______,_________;S矩形AEFG:S□ABCD=__________.
(2)□ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长;
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出AD、BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
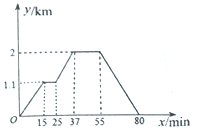
【题目】如图,反映的过程是小涛从家出发,去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小涛离家的距离.
(1)菜地离小涛家的距离是____km,小涛走到菜地用了____min,小涛给菜地浇水用了___min.
(2)菜地离玉米地的距离是____km,小涛从菜地到地用了____min,小涛给玉米地锄草用了____min.
(3)玉米地离小涛家的距离是___km,小涛从玉米地走回家的平均速度是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
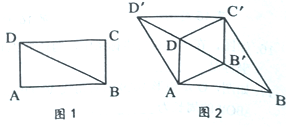
【题目】如图l,BD是矩形ABCD的对角线,∠ABD=30![]() ,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB’,C'D,AD’,BC’,如图2.
,AD=1.将△BCD沿射线BD方向平移到△B'C'D'的位置,使B'为BD中点,连接AB’,C'D,AD’,BC’,如图2.
(1)求证:四边形AB'C'D是菱形:
(2)四边形ABC'D'的周长为____:
(3)将四边形ABC'D’沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出可能拼成的矩形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=90°,射线OA绕点O逆时针方向以每秒6°的速度旋转(当旋转角度等于360°时,OA停止旋转),同时OB绕点O以每秒2°的速度旋转(当OA停止旋转时,OB同样停止旋转).求当OA旋转多少秒,旋转后的OA与OB形成的角度为50°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
求证:四边形ABEF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
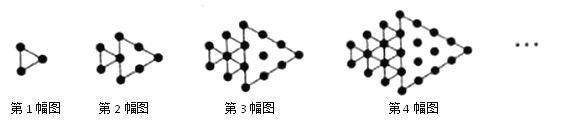
【题目】如图所示,将形状、大小完全相同的“![]() ”和线段按照一定规律摆成下列图形.第1幅图形中“
”和线段按照一定规律摆成下列图形.第1幅图形中“![]() ”的个数为
”的个数为![]() ,第2幅图形中“
,第2幅图形中“![]() ”的个数为
”的个数为![]() ,第3幅图形中“
,第3幅图形中“![]() ”的个数为
”的个数为![]() ,……,以此类推,解决以下问题:
,……,以此类推,解决以下问题:
(1)直接写出![]() ,
,![]() (用含n的代数式表示);
(用含n的代数式表示);
(2)猜想是否存在某幅图中“![]() ”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
(3)求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com